Ehrenfest equations
Encyclopedia
Ehrenfest
equations — equations which describe changes in specific heat capacity
and derivatives of specific volume
in second-order phase transitions. Clausius–Clapeyron relation does not make sense for second-order phase transitions, as both specific heat capacity
and specific volume
do not change in second-order phase transitions.
and specific volume 
, which are first derivatives of specific Gibbs free energy
- in second-order phase transitions. If we consider specific entropy
as a function of temperature
and pressure
, then its differential
is:
.
As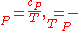
, then differential of specific entropy also is:
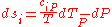
Where
and 
are the two phases which transit one into other. Due to continuity of specific entropy, the following holds in second-order phase transitions: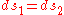 
. So,
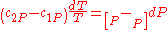
Therefore, the first Ehrenfest equation:
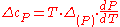
The second Ehrenfest equation is got in a like manner, but specific entropy is considered as function of temperature and specific volume:
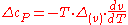
The third Ehrenfest equation is got in a like manner, but specific entropy is considered as function of
и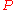 
.
Continuity of specific volume as of function of
and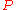 
gives the fourth Ehrenfest equation:
are not always finite. Transitions between different magnetic states of metals can't be described by Ehrenfest equations.
Paul Ehrenfest
Paul Ehrenfest was an Austrian and Dutch physicist, who made major contributions to the field of statistical mechanics and its relations with quantum mechanics, including the theory of phase transition and the Ehrenfest theorem.- Biography :Paul Ehrenfest was born and grew up in Vienna in a Jewish...
equations — equations which describe changes in specific heat capacity
Heat capacity
Heat capacity , or thermal capacity, is the measurable physical quantity that characterizes the amount of heat required to change a substance's temperature by a given amount...
and derivatives of specific volume
Specific volume
In thermodynamics, the specific volume of a substance is the ratio of the substance's volume to its mass. It is the reciprocal of density:In thermodynamics, the specific volume of a substance is the ratio of the substance's volume to its mass...
in second-order phase transitions. Clausius–Clapeyron relation does not make sense for second-order phase transitions, as both specific heat capacity
Heat capacity
Heat capacity , or thermal capacity, is the measurable physical quantity that characterizes the amount of heat required to change a substance's temperature by a given amount...
and specific volume
Specific volume
In thermodynamics, the specific volume of a substance is the ratio of the substance's volume to its mass. It is the reciprocal of density:In thermodynamics, the specific volume of a substance is the ratio of the substance's volume to its mass...
do not change in second-order phase transitions.
Quantitative consideration
Ehrenfest equations are the consequence of continuity of specific entropy and specific volume , which are first derivatives of specific Gibbs free energyGibbs free energy
In thermodynamics, the Gibbs free energy is a thermodynamic potential that measures the "useful" or process-initiating work obtainable from a thermodynamic system at a constant temperature and pressure...
- in second-order phase transitions. If we consider specific entropy
as a function of temperatureTemperature
Temperature is a physical property of matter that quantitatively expresses the common notions of hot and cold. Objects of low temperature are cold, while various degrees of higher temperatures are referred to as warm or hot...
and pressure
Pressure
Pressure is the force per unit area applied in a direction perpendicular to the surface of an object. Gauge pressure is the pressure relative to the local atmospheric or ambient pressure.- Definition :...
, then its differential
Differential of a function
In calculus, the differential represents the principal part of the change in a function y = ƒ with respect to changes in the independent variable. The differential dy is defined bydy = f'\,dx,...
is:
.As
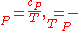, then differential of specific entropy also is: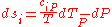Where
and are the two phases which transit one into other. Due to continuity of specific entropy, the following holds in second-order phase transitions: 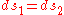. So,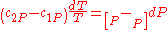Therefore, the first Ehrenfest equation:
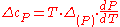
The second Ehrenfest equation is got in a like manner, but specific entropy is considered as function of temperature and specific volume:
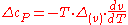
The third Ehrenfest equation is got in a like manner, but specific entropy is considered as function of
и 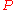.Continuity of specific volume as of function of
and 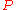gives the fourth Ehrenfest equation:Application
Derivatives of Gibbs free energyGibbs free energy
In thermodynamics, the Gibbs free energy is a thermodynamic potential that measures the "useful" or process-initiating work obtainable from a thermodynamic system at a constant temperature and pressure...
are not always finite. Transitions between different magnetic states of metals can't be described by Ehrenfest equations.