
Ehrenfeucht–Fraïssé game
Encyclopedia
In the mathematical discipline of model theory
, the Ehrenfeucht–Fraïssé game (also called back-and-forth games)
is a technique for determining whether two structure
s
are elementarily equivalent. The main application of Ehrenfeucht–Fraïssé games is in proving the inexpressibility of certain properties in first-order logic. Indeed, Ehrenfeucht–Fraïssé games provide a complete methodology for proving inexpressibility results for first-order logic. In this role, these games are of particular importance in finite model theory
and its applications in computer science (specifically Computer Aided Verification
and database theory
), since Ehrenfeucht–Fraïssé games are one of the such few techniques from model theory that remain valid in the context of finite models. Other widely used techniques for proving inexpressibility results, such as the compactness theorem
, do not work in finite models.
Ehrenfeucht–Fraïssé like games can also be defined for other logics, e.g. pebble game
s for finite variable logics and fixpoint logics.
The game lasts for a fixed amount of steps ( ) (an ordinal, but usually a finite number or
) (an ordinal, but usually a finite number or  ).
).

and , each with no function
, each with no function
symbols and the same set of relation
symbols,
and a fixed natural number
n. We can then define the Ehrenfeucht–Fraïssé
game to be a game between two players, Spoiler and Duplicator,
to be a game between two players, Spoiler and Duplicator,
played as follows:
It is easy to prove that if Duplicator wins this game for all n, then
 and
and  are elementarily
are elementarily
equivalent. If the set of relation symbols being considered is finite,
the converse is also true.
game to verify elementary equivalence was given by Roland Fraïssé
in his thesis;
it was formulated as a game by Andrzej Ehrenfeucht
.
The names Spoiler and Duplicator are due to Joel Spencer
. Other usual names are Eloise [sic] and Abelard (and often denoted by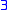 and
and  ) after Heloise and Abelard, a naming scheme introduced by Wilfrid Hodges
) after Heloise and Abelard, a naming scheme introduced by Wilfrid Hodges
in his book Model Theory.
Ehrenfeucht–Fraïssé game, and so do Chapters 6, 7, and 13 of Rosenstein's book on linear orders. A simple example of the Ehrenfeucht–Fraïssé game is given in
.
Phokion Kolaitis' slides and Neil Immerman
's book chapter on Ehrenfeucht–Fraïssé games discuss applications in computer science, the methodology theorem for proving inexpressibility results, and several simple inexpressibility proofs using this methodology.
Model theory
In mathematics, model theory is the study of mathematical structures using tools from mathematical logic....
, the Ehrenfeucht–Fraïssé game (also called back-and-forth games)
is a technique for determining whether two structure
Structure (mathematical logic)
In universal algebra and in model theory, a structure consists of a set along with a collection of finitary operations and relations which are defined on it....
s
are elementarily equivalent. The main application of Ehrenfeucht–Fraïssé games is in proving the inexpressibility of certain properties in first-order logic. Indeed, Ehrenfeucht–Fraïssé games provide a complete methodology for proving inexpressibility results for first-order logic. In this role, these games are of particular importance in finite model theory
Finite model theory
Finite Model Theory is a subarea of model theory . MT is the branch of mathematical logic which deals with the relation between a formal language and its interpretations . FMT is a restriction of MT to interpretations of finite structures, i.e...
and its applications in computer science (specifically Computer Aided Verification
Computer Aided Verification
Computer Aided Verification is an annual academic conference on the theory and practice of computer aided formal analysis of software and hardware systems. The conference consists of peer-reviewed research papers and system descriptions. The proceedings are published by Springer in the LNCS series...
and database theory
Database theory
Database theory encapsulates a broad range of topics related to the study and research of the theoretical realm of databases and database management systems....
), since Ehrenfeucht–Fraïssé games are one of the such few techniques from model theory that remain valid in the context of finite models. Other widely used techniques for proving inexpressibility results, such as the compactness theorem
Compactness theorem
In mathematical logic, the compactness theorem states that a set of first-order sentences has a model if and only if every finite subset of it has a model...
, do not work in finite models.
Ehrenfeucht–Fraïssé like games can also be defined for other logics, e.g. pebble game
Pebble game
In mathematics and computer science, a pebble game is a type of mathematical game played by moving "pebbles" or "markers" on a directed graph. A variety of different pebble games exist....
s for finite variable logics and fixpoint logics.
Main idea
The main idea behind the game is that we have two structures, and two players (defined below). One of the players wants to show that the two structures are different, whereas the other player wants to show that they are somewhat similar (according to first-order logic). The game is played in turns and rounds; A round proceeds as follows: First the first player (Spoiler) chooses any element from one of the structure, and the other player chooses an element from the other structure. The other player's task is to always pick an element that is "similar" to the one that Spoiler chose. The second player (Duplicator) wins if there exists an isomorphism between the elements chosen in the two different structures.The game lasts for a fixed amount of steps (
 ) (an ordinal, but usually a finite number or
) (an ordinal, but usually a finite number or  ).
).Definition
Suppose that we are given two structures
and
 , each with no function
, each with no functionFunction (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
symbols and the same set of relation
Relation (mathematics)
In set theory and logic, a relation is a property that assigns truth values to k-tuples of individuals. Typically, the property describes a possible connection between the components of a k-tuple...
symbols,
and a fixed natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
n. We can then define the Ehrenfeucht–Fraïssé
game
 to be a game between two players, Spoiler and Duplicator,
to be a game between two players, Spoiler and Duplicator,played as follows:
- The first player, Spoiler, picks either a member
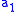 of
of  or a member
or a member 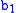 of
of  .
. - If Spoiler picked a member of
 , Duplicator picks a member
, Duplicator picks a member 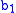 of
of  ; otherwise, Spoiler picked a member of
; otherwise, Spoiler picked a member of  , and Duplicator picks a member
, and Duplicator picks a member 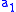 of
of  .
. - Spoiler picks either a member
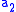 of
of  or a member
or a member  of
of  .
. - Duplicator picks an element
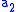 or
or  in whichever model wherefrom Spoiler did not pick.
in whichever model wherefrom Spoiler did not pick. - Spoiler and Duplicator continue to pick members of
 and
and  for
for  more steps.
more steps. - At the conclusion of the game, we have chosen distinct elements
 of
of  and
and 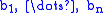 of
of  . We therefore have two structures on the set
. We therefore have two structures on the set  , one induced from
, one induced from  via the map sending
via the map sending 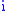 to
to 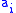 , and the other induced from
, and the other induced from  via the map sending
via the map sending 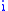 to
to  . Duplicator wins if these structures are the same; Spoiler wins if they are not.
. Duplicator wins if these structures are the same; Spoiler wins if they are not.
It is easy to prove that if Duplicator wins this game for all n, then
 and
and  are elementarily
are elementarilyequivalent. If the set of relation symbols being considered is finite,
the converse is also true.
History
The back-and-forth method used in the Ehrenfeucht-Fraïsségame to verify elementary equivalence was given by Roland Fraïssé
Roland Fraïssé
Roland Fraïssé was a French mathematical logician. He received his doctoral degree from the University of Paris in 1953. In his thesis, Fraïssé used the back-and-forth method to determine whether two model-theoretic structures were elementarily equivalent...
in his thesis;
it was formulated as a game by Andrzej Ehrenfeucht
Andrzej Ehrenfeucht
Andrzej Ehrenfeucht is a Polish American mathematician and computer scientist. He formulated the Ehrenfeucht–Fraïssé game, using the back-and-forth method given by Roland Fraïssé in his thesis. The Ehrenfeucht–Mycielski sequence is also named after him....
.
The names Spoiler and Duplicator are due to Joel Spencer
Joel Spencer
Joel Spencer is an American mathematician. He is a combinatorialist who has worked on probabilistic methods in combinatorics and on Ramsey theory. He received his doctorate from Harvard University in 1970, under the supervision of Andrew Gleason...
. Other usual names are Eloise [sic] and Abelard (and often denoted by
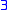 and
and  ) after Heloise and Abelard, a naming scheme introduced by Wilfrid Hodges
) after Heloise and Abelard, a naming scheme introduced by Wilfrid HodgesWilfrid Hodges
Wilfrid Augustine Hodges is a British mathematician, known for his work in model theory. He was Professor of Mathematics at Queen Mary, University of London from 1987 to 2006, and is the author of numerous books on logic....
in his book Model Theory.
Further reading
Chapter 1 of Poizat's model theory text contains an introduction to theEhrenfeucht–Fraïssé game, and so do Chapters 6, 7, and 13 of Rosenstein's book on linear orders. A simple example of the Ehrenfeucht–Fraïssé game is given in
.
Phokion Kolaitis' slides and Neil Immerman
Neil Immerman
Neil Immerman is an American theoretical computer scientist, a professor of computer science at the University of Massachusetts Amherst...
's book chapter on Ehrenfeucht–Fraïssé games discuss applications in computer science, the methodology theorem for proving inexpressibility results, and several simple inexpressibility proofs using this methodology.

