
Eigenform
Encyclopedia
An eigenform is a modular form
which is an eigenvector for all Hecke operator
s Tm, m = 1, 2, 3, ….
Eigenforms fall into the realm of number theory
, but can be found in other areas of math and science such as analysis
, combinatorics
, and physics
.
is one:
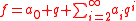
where q = e2πiz, and ai, i ≥ 1 turn out to be the eigenvalues of f corresponding to the Hecke operator Ti. In the case of that f is not a cusp form, the eigenvalues can be given explicitly.
, an eigenform can be normalized with respect to its inner product: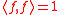
is not the full SL(2,Z), there is not a Hecke operator for each n ∈ Z, and as such the definition of an eigenform is changed accordingly: an eigenform is a modular form which is a simultaneous eigenvector for all Hecke operators that act on the space.
*
Modular form
In mathematics, a modular form is a analytic function on the upper half-plane satisfying a certain kind of functional equation and growth condition. The theory of modular forms therefore belongs to complex analysis but the main importance of the theory has traditionally been in its connections...
which is an eigenvector for all Hecke operator
Hecke operator
In mathematics, in particular in the theory of modular forms, a Hecke operator, studied by , is a certain kind of "averaging" operator that plays a significant role in the structure of vector spaces of modular forms and more general automorphic representations....
s Tm, m = 1, 2, 3, ….
Eigenforms fall into the realm of number theory
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, but can be found in other areas of math and science such as analysis
Analysis
Analysis is the process of breaking a complex topic or substance into smaller parts to gain a better understanding of it. The technique has been applied in the study of mathematics and logic since before Aristotle , though analysis as a formal concept is a relatively recent development.The word is...
, combinatorics
Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
, and physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
.
Normalization
There are two different normalizations for an eigenform (or for a modular form in general).Algebraic normalization
An eigenform is said to be normalized when scaled so that the q-coefficient in its Fourier seriesFourier series
In mathematics, a Fourier series decomposes periodic functions or periodic signals into the sum of a set of simple oscillating functions, namely sines and cosines...
is one:
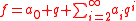
where q = e2πiz, and ai, i ≥ 1 turn out to be the eigenvalues of f corresponding to the Hecke operator Ti. In the case of that f is not a cusp form, the eigenvalues can be given explicitly.
Analytic normalization
As in any inner product spaceInner product space
In mathematics, an inner product space is a vector space with an additional structure called an inner product. This additional structure associates each pair of vectors in the space with a scalar quantity known as the inner product of the vectors...
, an eigenform can be normalized with respect to its inner product:
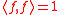
Higher levels
In the case that the modular groupModular group
In mathematics, the modular group Γ is a fundamental object of study in number theory, geometry, algebra, and many other areas of advanced mathematics...
is not the full SL(2,Z), there is not a Hecke operator for each n ∈ Z, and as such the definition of an eigenform is changed accordingly: an eigenform is a modular form which is a simultaneous eigenvector for all Hecke operators that act on the space.
*

