
Eilenberg's inequality
Encyclopedia
Eilenberg's inequality is a mathematical inequality for Lipschitz-continuous function
s.
Let ƒ : X → Y be a Lipschitz-continuous function between separable metric space
s whose Lipschitz constant is denoted by Lip ƒ. Then, Eilenberg's inequality states that
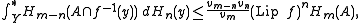
for any A ⊂ X and all 0 ≤ n ≤ m, where
Lipschitz continuity
In mathematical analysis, Lipschitz continuity, named after Rudolf Lipschitz, is a strong form of uniform continuity for functions. Intuitively, a Lipschitz continuous function is limited in how fast it can change: for every pair of points on the graph of this function, the absolute value of the...
s.
Let ƒ : X → Y be a Lipschitz-continuous function between separable metric space
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
s whose Lipschitz constant is denoted by Lip ƒ. Then, Eilenberg's inequality states that
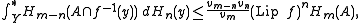
for any A ⊂ X and all 0 ≤ n ≤ m, where
- the asterisk denotes the upper Lebesgue integral,
- vn is the volume of the unit ball in Rn,
- Hn is the n-dimensional Hausdorff measureHausdorff measureIn mathematics a Hausdorff measure is a type of outer measure, named for Felix Hausdorff, that assigns a number in [0,∞] to each set in Rn or, more generally, in any metric space. The zero dimensional Hausdorff measure is the number of points in the set or ∞ if the set is infinite...
.

