Eilenberg–Zilber theorem
Encyclopedia
In mathematics
, specifically in algebraic topology
, the Eilenberg–Zilber theorem is an important result in establishing the link between the homology groups of a product space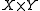
and those of the spaces 
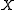and 
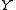. The theorem first appeared in a 1953 paper in the American Journal of Mathematics
.
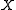and 
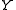are topological spaces, Then we have the three chain complexes 
, 
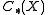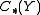, and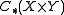 
. (The argument applies equally to the simplicial or singular chain complexes.) We also have the tensor product complex 
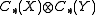, whose differential is, by definition,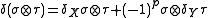
for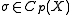
and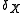 
, 
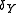the differentials on 
,
.
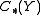Then the theorem says that we have a chain maps
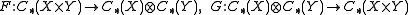
such that
is the identity and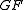 
is chain-homotopic to the identity. Moreover, the maps are natural
in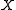
and 
. Consequently the two complexes must have the same homology:
An important generalisation to the nonabelian case using crossed complexes is given in the paper by Tonks below. This give full details of a result on the (simplicial) classifying space
of a crossed complex stated but not proved in the paper by Brown and Higgins on classifying spaces.
, which expresses the homology groups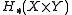
in terms of 
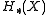and 
. In light of the Eilenberg–Zilber theorem, the content of the Künneth theorem consists in analysing how the homology of the tensor product complex relates to the homologies of the factors; the answer is somewhat subtle.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, specifically in algebraic topology
Algebraic topology
Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
, the Eilenberg–Zilber theorem is an important result in establishing the link between the homology groups of a product space
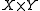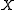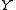and those of the spaces and . The theorem first appeared in a 1953 paper in the American Journal of MathematicsAmerican Journal of Mathematics
The American Journal of Mathematics is a bimonthly mathematics journal published by the Johns Hopkins University Press.- History :The American Journal of Mathematics is the oldest continuously-published mathematical journal in the United States, established in 1878 at the Johns Hopkins University...
.
Statement of the theorem
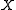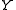The theorem can be formulated as follows. Suppose and are topological spaces, Then we have the three chain complexes 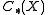, , 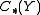and 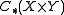. (The argument applies equally to the simplicial or singular chain complexes.) We also have the tensor product complex 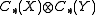, whose differential is, by definition,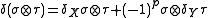for
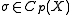and 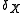, 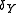the differentials on ,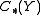.Then the theorem says that we have a chain maps
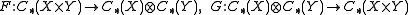
such that
is the identity and 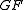is chain-homotopic to the identity. Moreover, the maps are naturalNatural transformation
In category theory, a branch of mathematics, a natural transformation provides a way of transforming one functor into another while respecting the internal structure of the categories involved. Hence, a natural transformation can be considered to be a "morphism of functors". Indeed this intuition...
in
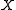and . Consequently the two complexes must have the same homology:An important generalisation to the nonabelian case using crossed complexes is given in the paper by Tonks below. This give full details of a result on the (simplicial) classifying space
Classifying space
In mathematics, specifically in homotopy theory, a classifying space BG of a topological group G is the quotient of a weakly contractible space EG by a free action of G...
of a crossed complex stated but not proved in the paper by Brown and Higgins on classifying spaces.
Consequences
The Eilenberg–Zilber theorem is a key ingredient in establishing the Künneth theoremKünneth theorem
In mathematics, especially in homological algebra and algebraic topology, a Künneth theorem is a statement relating the homology of two objects to the homology of their product. The classical statement of the Künneth theorem relates the singular homology of two topological spaces X and Y and their...
, which expresses the homology groups
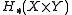in terms of 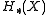and . In light of the Eilenberg–Zilber theorem, the content of the Künneth theorem consists in analysing how the homology of the tensor product complex relates to the homologies of the factors; the answer is somewhat subtle.