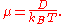Einstein relation (kinetic theory)
Encyclopedia
In physics
(namely, in kinetic theory
) the Einstein relation (also known as Einstein–Smoluchowski relation) is a previously unexpected connection revealed independently by Albert Einstein
in 1905 and by Marian Smoluchowski
(1906) in their papers on Brownian motion
. Two important special cases of the relation are:
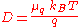(diffusion of charged
particles)
("Einstein–Stokes equation", for diffusion of spherical particles through liquid with low Reynolds number)
where
The more general form of the equation is: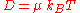
where the "mobility" μ is the ratio of the particle's terminal drift velocity
to an applied force
, μ = vd / F.
This equation is an early example of a fluctuation-dissipation relation
. It is frequently used in the electrodiffusion phenomena.
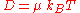
is in the case of a charged particle: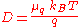
is the inverse of the drag coefficient 
. A damping constant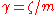 
is frequently used for the momentum relaxation time (time needed for the inertia momentum to become negligible compared to the random momenta) of the diffusive object. For spherical particles of radius 
, Stokes' law
gives
where
is the viscosity
of the medium. Thus the Einstein-Smoluchowski relation results into the Einstein-Stokes relation
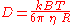
with an arbitrary density of states
the Einstein relation is:
where
is the chemical potential
and p the particle number
.
. Essentially the same proof is found in many places, for example see Kubo.)
Suppose some potential energy
U creates a force on the particle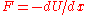
(for example, an electric force). We assume that the particle would respond, other things equal, by moving with velocity 
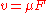. Now assume that there are a large number of such particles, with concentration 
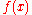as a function of position. After some time, equilibrium will be established: The particles will "pile up" around the areas with lowest U, but will still be spread out to some extent because of random diffusion. At this point, there is no net flow of particles: The tendency of particles to get pulled towards lower U (called the "drift current") is equal and opposite the tendency of particles to spread out due to diffusion (called the "diffusion current").
The net flow of particles due to the drift current alone is
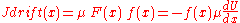
(i.e. the number of particles flowing past a point is the particle concentration times the average velocity.)
The net flow of particles due to the diffusion current alone is, by Fick's laws
(the minus sign means that particles flow from higher concentration to lower).
Equilibrium requires:
In equilibrium, we can apply thermodynamics, in particular Boltzmann statistics, to infer that
where A is some constant related to the total number of particles. Therefore, by the chain rule
,
Finally, plugging this in:
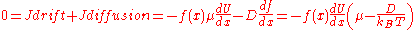
Since this equation must hold everywhere,
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
(namely, in kinetic theory
Kinetic theory
The kinetic theory of gases describes a gas as a large number of small particles , all of which are in constant, random motion. The rapidly moving particles constantly collide with each other and with the walls of the container...
) the Einstein relation (also known as Einstein–Smoluchowski relation) is a previously unexpected connection revealed independently by Albert Einstein
Albert Einstein
Albert Einstein was a German-born theoretical physicist who developed the theory of general relativity, effecting a revolution in physics. For this achievement, Einstein is often regarded as the father of modern physics and one of the most prolific intellects in human history...
in 1905 and by Marian Smoluchowski
Marian Smoluchowski
Marian Smoluchowski was an ethnic Polish scientist in the Austro-Hungarian Empire. He was a pioneer of statistical physics and an avid mountaineer.-Life:...
(1906) in their papers on Brownian motion
Brownian motion
Brownian motion or pedesis is the presumably random drifting of particles suspended in a fluid or the mathematical model used to describe such random movements, which is often called a particle theory.The mathematical model of Brownian motion has several real-world applications...
. Two important special cases of the relation are:
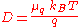(diffusion of chargedElectric charge
Electric charge is a physical property of matter that causes it to experience a force when near other electrically charged matter. Electric charge comes in two types, called positive and negative. Two positively charged substances, or objects, experience a mutual repulsive force, as do two...
particles)
("Einstein–Stokes equation", for diffusion of spherical particles through liquid with low Reynolds number)where
- D is the diffusion constantFick's law of diffusionFick's laws of diffusion describe diffusion and can be used to solve for the diffusion coefficient, D. They were derived by Adolf Fick in the year 1855.- Fick's first law :...
, - q is the electrical charge of a particle,
- μq, the electrical mobilityElectrical mobilityElectrical mobility is the ability of charged particles to move through a medium in response to an electric field that is pulling them...
of the charged particle, i.e. the ratio of the particle's terminal drift velocityDrift velocityThe drift velocity is the average velocity that a particle, such as an electron, attains due to an electric field. It can also be referred to as Axial Drift Velocity since particles defined are assumed to be moving along a plane. In general, an electron will 'rattle around' in a conductor at the...
to an applied electric fieldElectric fieldIn physics, an electric field surrounds electrically charged particles and time-varying magnetic fields. The electric field depicts the force exerted on other electrically charged objects by the electrically charged particle the field is surrounding...
, 
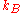is Boltzmann's constant,- T is the absolute temperature,
- η is viscosityViscosityViscosity is a measure of the resistance of a fluid which is being deformed by either shear or tensile stress. In everyday terms , viscosity is "thickness" or "internal friction". Thus, water is "thin", having a lower viscosity, while honey is "thick", having a higher viscosity...
- r is the radius of the spherical particle.
The more general form of the equation is:
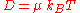
where the "mobility" μ is the ratio of the particle's terminal drift velocity
Drift velocity
The drift velocity is the average velocity that a particle, such as an electron, attains due to an electric field. It can also be referred to as Axial Drift Velocity since particles defined are assumed to be moving along a plane. In general, an electron will 'rattle around' in a conductor at the...
to an applied force
Force
In physics, a force is any influence that causes an object to undergo a change in speed, a change in direction, or a change in shape. In other words, a force is that which can cause an object with mass to change its velocity , i.e., to accelerate, or which can cause a flexible object to deform...
, μ = vd / F.
This equation is an early example of a fluctuation-dissipation relation
Fluctuation dissipation theorem
The fluctuation-dissipation theorem is a powerful tool in statistical physics for predicting the behavior of non-equilibrium thermodynamical systems. These systems involve the irreversible dissipation of energy into heat from their reversible thermal fluctuations at thermodynamic equilibrium...
. It is frequently used in the electrodiffusion phenomena.
Electrical mobility equation
For a particle with charge q, its electrical mobility μq is related to its generalized mobility μ by the equation μ=μq/q. Therefore, the general form of the equation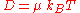is in the case of a charged particle:
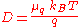
Einstein–Stokes equation
In the limit of low Reynolds number, the mobility is the inverse of the drag coefficient . A damping constant 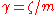is frequently used for the momentum relaxation time (time needed for the inertia momentum to become negligible compared to the random momenta) of the diffusive object. For spherical particles of radius , Stokes' lawStokes' law
In 1851, George Gabriel Stokes derived an expression, now known as Stokes' law, for the frictional force – also called drag force – exerted on spherical objects with very small Reynolds numbers in a continuous viscous fluid...
gives
where
is the viscosityViscosity
Viscosity is a measure of the resistance of a fluid which is being deformed by either shear or tensile stress. In everyday terms , viscosity is "thickness" or "internal friction". Thus, water is "thin", having a lower viscosity, while honey is "thick", having a higher viscosity...
of the medium. Thus the Einstein-Smoluchowski relation results into the Einstein-Stokes relation
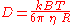
Semiconductor
In a semiconductorSemiconductor
A semiconductor is a material with electrical conductivity due to electron flow intermediate in magnitude between that of a conductor and an insulator. This means a conductivity roughly in the range of 103 to 10−8 siemens per centimeter...
with an arbitrary density of states
Density of states
In solid-state and condensed matter physics, the density of states of a system describes the number of states per interval of energy at each energy level that are available to be occupied by electrons. Unlike isolated systems, like atoms or molecules in gas phase, the density distributions are not...
the Einstein relation is:
where
is the chemical potentialChemical potential
Chemical potential, symbolized by μ, is a measure first described by the American engineer, chemist and mathematical physicist Josiah Willard Gibbs. It is the potential that a substance has to produce in order to alter a system...
and p the particle number
Particle number
The particle number of a thermodynamic system, conventionally indicated with the letter N, is the number of constituent particles in that system. The particle number is a fundamental parameter in thermodynamics which is conjugate to the chemical potential. Unlike most physical quantities, particle...
.
Proof of general case
(This is a proof in one dimension, but it is identical to a proof in two or three dimensions: Just replace d/dx with. Essentially the same proof is found in many places, for example see Kubo.)Suppose some potential energy
Potential energy
In physics, potential energy is the energy stored in a body or in a system due to its position in a force field or due to its configuration. The SI unit of measure for energy and work is the Joule...
U creates a force on the particle
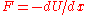(for example, an electric force). We assume that the particle would respond, other things equal, by moving with velocity 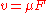. Now assume that there are a large number of such particles, with concentration 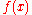as a function of position. After some time, equilibrium will be established: The particles will "pile up" around the areas with lowest U, but will still be spread out to some extent because of random diffusion. At this point, there is no net flow of particles: The tendency of particles to get pulled towards lower U (called the "drift current") is equal and opposite the tendency of particles to spread out due to diffusion (called the "diffusion current").The net flow of particles due to the drift current alone is
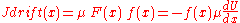
(i.e. the number of particles flowing past a point is the particle concentration times the average velocity.)
The net flow of particles due to the diffusion current alone is, by Fick's laws
(the minus sign means that particles flow from higher concentration to lower).
Equilibrium requires:
In equilibrium, we can apply thermodynamics, in particular Boltzmann statistics, to infer that
where A is some constant related to the total number of particles. Therefore, by the chain rule
Chain rule
In calculus, the chain rule is a formula for computing the derivative of the composition of two or more functions. That is, if f is a function and g is a function, then the chain rule expresses the derivative of the composite function in terms of the derivatives of f and g.In integration, the...
,
Finally, plugging this in:
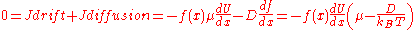
Since this equation must hold everywhere,
