
Engel theorem
Encyclopedia
In representation theory
, Engel's theorem is one of the basic theorems in the theory of Lie algebra
s; it asserts that for a Lie algebra two concepts of nilpotency
are identical. A useful form of the theorem says that if a Lie algebra L of matrices consists of nilpotent matrices, then they can all be simultaneously brought to a strictly upper triangular form. The theorem is named after the mathematician Friedrich Engel
, who sketched a proof of it in a letter to Killing dated 20 July 1890 . Engel's student Umlauf gave a complete proof in his 1891 dissertation, reprinted as .
A linear operator T on a vector space V is defined to be nilpotent if there is a positive integer k such that Tk = 0. For example, any operator given by a matrix whose entries are zero on and below its diagonal is nilpotent.

An element x of a Lie algebra L is ad-nilpotent if and only if the linear operator on L defined by
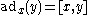
is nilpotent. Note that in the Lie algebra L(V) of linear operators on V, the identity operator IV is ad-nilpotent (because ) but is not a nilpotent operator.
) but is not a nilpotent operator.
A Lie algebra L is nilpotent if and only if the lower central series defined recursively
by
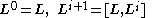
eventually reaches {0}.
Theorem. A finite-dimensional Lie algebra L is nilpotent if and only if every element of L is ad-nilpotent.
Note that no assumption on the underlying base field is required.
The key lemma in the proof of Engel's theorem is the following fact
about Lie algebras of linear operators on finite dimensional vector spaces which is useful in its own right:
Let L be a Lie subalgebra of L(V). Then L consists of nilpotent operators if and only if there is a sequence

of subspaces of V such that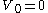 ,
, 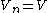 and
and
Thus Lie algebras of nilpotent operators are simultaneously strictly upper-triangulizable.
Representation theory
Representation theory is a branch of mathematics that studies abstract algebraic structures by representing their elements as linear transformations of vector spaces, and studiesmodules over these abstract algebraic structures...
, Engel's theorem is one of the basic theorems in the theory of Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
s; it asserts that for a Lie algebra two concepts of nilpotency
Nilpotent
In mathematics, an element x of a ring R is called nilpotent if there exists some positive integer n such that xn = 0....
are identical. A useful form of the theorem says that if a Lie algebra L of matrices consists of nilpotent matrices, then they can all be simultaneously brought to a strictly upper triangular form. The theorem is named after the mathematician Friedrich Engel
Friedrich Engel (mathematician)
Friedrich Engel was a German mathematician.Engel was born in Lugau, Saxony, as the son of a Lutheran pastor. He attended the Universities of both Leipzig and Berlin, before receiving his doctorate from Leipzig in 1883.Engel studied under Felix Klein at Leipzig, and collaborated with Sophus Lie for...
, who sketched a proof of it in a letter to Killing dated 20 July 1890 . Engel's student Umlauf gave a complete proof in his 1891 dissertation, reprinted as .
A linear operator T on a vector space V is defined to be nilpotent if there is a positive integer k such that Tk = 0. For example, any operator given by a matrix whose entries are zero on and below its diagonal is nilpotent.

An element x of a Lie algebra L is ad-nilpotent if and only if the linear operator on L defined by
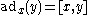
is nilpotent. Note that in the Lie algebra L(V) of linear operators on V, the identity operator IV is ad-nilpotent (because
 ) but is not a nilpotent operator.
) but is not a nilpotent operator.A Lie algebra L is nilpotent if and only if the lower central series defined recursively
Recursion
Recursion is the process of repeating items in a self-similar way. For instance, when the surfaces of two mirrors are exactly parallel with each other the nested images that occur are a form of infinite recursion. The term has a variety of meanings specific to a variety of disciplines ranging from...
by
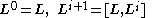
eventually reaches {0}.
Theorem. A finite-dimensional Lie algebra L is nilpotent if and only if every element of L is ad-nilpotent.
Note that no assumption on the underlying base field is required.
The key lemma in the proof of Engel's theorem is the following fact
about Lie algebras of linear operators on finite dimensional vector spaces which is useful in its own right:
Let L be a Lie subalgebra of L(V). Then L consists of nilpotent operators if and only if there is a sequence

of subspaces of V such that
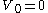 ,
, 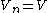 and
andThus Lie algebras of nilpotent operators are simultaneously strictly upper-triangulizable.


