
Enneper-Weierstrass parameterization
Encyclopedia
In mathematics
, the Weierstrass–Enneper parameterization of minimal surface
s is a classical piece of differential geometry.
Alfred Enneper
and Karl Weierstrass
studied minimal surfaces as far back as 1863.
Let ƒ and g be functions on either the entire complex plane or the unit disk, where g is meromorphic
and ƒ is analytic
, such that wherever g has a pole of order m, f has a zero of order 2m (or equivalently, such that the product ƒg2 is holomorphic), and let c1, c2, c3 be constants. Then the surface with coordinates (x1,x2,x3) is minimal, where the xk are defined using the real part of a complex integral, as follows:
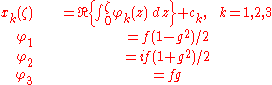
The converse is also true: every nonplanar minimal surface defined over a simply connected domain can be given a parametrization of this type.
For example, Enneper's surface has ƒ(z) = 1, g(z) = z.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Weierstrass–Enneper parameterization of minimal surface
Minimal surface
In mathematics, a minimal surface is a surface with a mean curvature of zero.These include, but are not limited to, surfaces of minimum area subject to various constraints....
s is a classical piece of differential geometry.
Alfred Enneper
Alfred Enneper
Alfred Enneper earned his PhD from the Georg-August-Universität Göttingen in 1856 for his dissertation about functions with complex arguments. After his habilitation 1859 in Göttingen he was from 1870 on Professor at Göttingen. He studied minimal surfaces and parametrized Enneper's minimal...
and Karl Weierstrass
Karl Weierstrass
Karl Theodor Wilhelm Weierstrass was a German mathematician who is often cited as the "father of modern analysis".- Biography :Weierstrass was born in Ostenfelde, part of Ennigerloh, Province of Westphalia....
studied minimal surfaces as far back as 1863.
Let ƒ and g be functions on either the entire complex plane or the unit disk, where g is meromorphic
Meromorphic function
In complex analysis, a meromorphic function on an open subset D of the complex plane is a function that is holomorphic on all D except a set of isolated points, which are poles for the function...
and ƒ is analytic
Analytic function
In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...
, such that wherever g has a pole of order m, f has a zero of order 2m (or equivalently, such that the product ƒg2 is holomorphic), and let c1, c2, c3 be constants. Then the surface with coordinates (x1,x2,x3) is minimal, where the xk are defined using the real part of a complex integral, as follows:
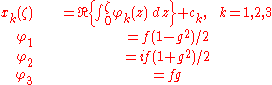
The converse is also true: every nonplanar minimal surface defined over a simply connected domain can be given a parametrization of this type.
For example, Enneper's surface has ƒ(z) = 1, g(z) = z.

