Equation of State Calculations by Fast Computing Machines
Encyclopedia
Equation of State Calculations by Fast Computing Machines is an article published by Nicholas Metropolis
, Arianna W. Rosenbluth, Marshall N. Rosenbluth, Augusta H. Teller, and Edward Teller
in the Journal of Chemical Physics
in 1953. This paper proposed what became known as the Metropolis Monte Carlo algorithm, which forms the basis for Monte Carlo statistical mechanics
simulations of atomic and molecular systems. The attribution of the method to Metropolis is unfortunate, as "Metropolis played no role in its development other than providing computer time". In fact, the theoretical work was done by Marshall N. Rosenbluth, who later gained renown as one of the greatest plasma physicists of the 20th century.
Monte Carlo methods are a class of computational algorithms that rely on repeated random sampling to compute their results. In statistical mechanics applications prior to the introduction of the Metropolis algorithm, the method consisted of generating a large number of random configurations of the system, computing the properties of interest (such as energy or density) for each configuration, and then producing a weighted average where the weight of each configuration is its Boltzmann factor
, exp(−E/kT), where E is the energy
, T is the temperature
, and k is Boltzmann's constant. The key contribution of the Metropolis paper was the idea that
 This change makes the sampling focus on the low-energy configurations, which contribute the most to the Boltzmann average, resulting in improved convergence
This change makes the sampling focus on the low-energy configurations, which contribute the most to the Boltzmann average, resulting in improved convergence
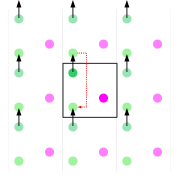
. To choose configurations with a probability exp(−E/kT) that can be weighed evenly, the authors devised the following algorithm: 1) each configuration is generated by a random move on the previous configuration and the new energy is computed; 2) if the new energy is lower, the move is always accepted; otherwise the move is accepted with a probability of exp(−ΔE/kT). When a move is rejected, the last accepted configuration is counted again for the statistical averages and is used as a base for the next attempted move.
The main topic of the article was the numerical calculation of the equation of state
for a system of rigid spheres in two dimensions. Subsequent work generalized the method to three dimensions and to fluids using the Lennard-Jones potential
. The simulations were done for a system of 224 particles; each simulation consisted of up to 48 cycles, where each cycle consisted of moving each particle once and took about three minutes of computer time using the MANIAC
computer at Los Alamos National Lab.
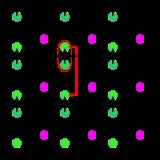
To minimize surface effects, the authors introduced the use of periodic boundary conditions
. This means that the simulated system is treated as a unit cell in a lattice, and when a particle moves out of the cell, it automatically comes in through the other side.
According to a perspective published nearly fifty years later by William L. Jorgensen
, "Metropolis et al. introduced the samplic method and periodic boundary conditions that remain at the heart of Monte Carlo statistical mechanics simulations of fluids. This was one of the major contributions to theoretical chemistry of the twentieth century." As of 2011, the article has been cited over 18,000 times.
In another perspective, it was said that although "the Metropolis algorithm began as a technique for attacking specific problems in numerical simulations of physical systems [...] later, the subject exploded as the scope of applications broadened in many surprising directions, including function minimization, computational geometry, and combinatorial counting. Today, topics related to the Metropolis algorithm constitute an entire field of computational science supported by a deep theory and having applications ranging from physical simulations to the foundations of computational complexity."
Nicholas Metropolis
Nicholas Constantine Metropolis was a Greek American physicist.-Work:Metropolis received his B.Sc. and Ph.D. degrees in physics at the University of Chicago...
, Arianna W. Rosenbluth, Marshall N. Rosenbluth, Augusta H. Teller, and Edward Teller
Edward Teller
Edward Teller was a Hungarian-American theoretical physicist, known colloquially as "the father of the hydrogen bomb," even though he did not care for the title. Teller made numerous contributions to nuclear and molecular physics, spectroscopy , and surface physics...
in the Journal of Chemical Physics
Journal of Chemical Physics
The Journal of Chemical Physics is a scientific journal that publishes research papers on all areas of chemical physics. Two volumes, each of 24 issues, are published per year. It is published by the American Institute of Physics. The editors have been:...
in 1953. This paper proposed what became known as the Metropolis Monte Carlo algorithm, which forms the basis for Monte Carlo statistical mechanics
Statistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
simulations of atomic and molecular systems. The attribution of the method to Metropolis is unfortunate, as "Metropolis played no role in its development other than providing computer time". In fact, the theoretical work was done by Marshall N. Rosenbluth, who later gained renown as one of the greatest plasma physicists of the 20th century.
Monte Carlo methods are a class of computational algorithms that rely on repeated random sampling to compute their results. In statistical mechanics applications prior to the introduction of the Metropolis algorithm, the method consisted of generating a large number of random configurations of the system, computing the properties of interest (such as energy or density) for each configuration, and then producing a weighted average where the weight of each configuration is its Boltzmann factor
Boltzmann factor
In physics, the Boltzmann factor is a weighting factor that determines the relative probability of a particle to be in a state i in a multi-state system in thermodynamic equilibrium at temperature T...
, exp(−E/kT), where E is the energy
Energy
In physics, energy is an indirectly observed quantity. It is often understood as the ability a physical system has to do work on other physical systems...
, T is the temperature
Temperature
Temperature is a physical property of matter that quantitatively expresses the common notions of hot and cold. Objects of low temperature are cold, while various degrees of higher temperatures are referred to as warm or hot...
, and k is Boltzmann's constant. The key contribution of the Metropolis paper was the idea that

Limit of a sequence
The limit of a sequence is, intuitively, the unique number or point L such that the terms of the sequence become arbitrarily close to L for "large" values of n...
. To choose configurations with a probability exp(−E/kT) that can be weighed evenly, the authors devised the following algorithm: 1) each configuration is generated by a random move on the previous configuration and the new energy is computed; 2) if the new energy is lower, the move is always accepted; otherwise the move is accepted with a probability of exp(−ΔE/kT). When a move is rejected, the last accepted configuration is counted again for the statistical averages and is used as a base for the next attempted move.
The main topic of the article was the numerical calculation of the equation of state
Equation of state
In physics and thermodynamics, an equation of state is a relation between state variables. More specifically, an equation of state is a thermodynamic equation describing the state of matter under a given set of physical conditions...
for a system of rigid spheres in two dimensions. Subsequent work generalized the method to three dimensions and to fluids using the Lennard-Jones potential
Lennard-Jones potential
The Lennard-Jones potential is a mathematically simple model that approximates the interaction between a pair of neutral atoms or molecules. A form of the potential was first proposed in 1924 by John Lennard-Jones...
. The simulations were done for a system of 224 particles; each simulation consisted of up to 48 cycles, where each cycle consisted of moving each particle once and took about three minutes of computer time using the MANIAC
Maniac
Maniac may refer to:*A person who exhibits the behaviour known as mania*A classification of serial killer*MANIAC I, an early computer...
computer at Los Alamos National Lab.
To minimize surface effects, the authors introduced the use of periodic boundary conditions
Periodic boundary conditions
In mathematical models and computer simulations, periodic boundary conditions are a set of boundary conditions that are often used to simulate a large system by modelling a small part that is far from its edge...
. This means that the simulated system is treated as a unit cell in a lattice, and when a particle moves out of the cell, it automatically comes in through the other side.
According to a perspective published nearly fifty years later by William L. Jorgensen
William L. Jorgensen
William L. Jorgensen is a Sterling Professor of Chemistry at Yale University. He is considered a pioneer in the field of computational chemistry...
, "Metropolis et al. introduced the samplic method and periodic boundary conditions that remain at the heart of Monte Carlo statistical mechanics simulations of fluids. This was one of the major contributions to theoretical chemistry of the twentieth century." As of 2011, the article has been cited over 18,000 times.
In another perspective, it was said that although "the Metropolis algorithm began as a technique for attacking specific problems in numerical simulations of physical systems [...] later, the subject exploded as the scope of applications broadened in many surprising directions, including function minimization, computational geometry, and combinatorial counting. Today, topics related to the Metropolis algorithm constitute an entire field of computational science supported by a deep theory and having applications ranging from physical simulations to the foundations of computational complexity."

