
Erdos–Woods number
Encyclopedia
In number theory
, an Erdős–Woods number is a positive integer that has the following property:
Consider a sequence of consecutive positive integers . The number k is an Erdős–Woods number if there exists such a sequence, beginning with some number a, in which each of the elements has a common factor with one of the endpoints. In other words, if there exists a positive integer a such that for each integer i,
. The number k is an Erdős–Woods number if there exists such a sequence, beginning with some number a, in which each of the elements has a common factor with one of the endpoints. In other words, if there exists a positive integer a such that for each integer i, 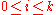 , either
, either  or
or 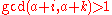 .
.
The first few Erdős–Woods numbers are:
(Arguably 0 and 1 could also be included as trivial entries.)
Investigation of such numbers stemmed from a prior conjecture by Paul Erdős
:
Alan R. Woods investigated this for his 1981 thesis, and conjectured that whenever k > 1, the interval always included a number coprime
always included a number coprime
to both endpoints. It was only later that he found the first counterexample,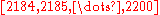 with k = 16.
with k = 16.
David L. Dowe proved
that there are infinitely many Erdős–Woods numbers, and Cégielski, Heroult and Richard showed that the set is recursive.
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, an Erdős–Woods number is a positive integer that has the following property:
Consider a sequence of consecutive positive integers
 . The number k is an Erdős–Woods number if there exists such a sequence, beginning with some number a, in which each of the elements has a common factor with one of the endpoints. In other words, if there exists a positive integer a such that for each integer i,
. The number k is an Erdős–Woods number if there exists such a sequence, beginning with some number a, in which each of the elements has a common factor with one of the endpoints. In other words, if there exists a positive integer a such that for each integer i, 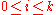 , either
, either  or
or 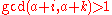 .
.The first few Erdős–Woods numbers are:
- 1616 (number)16 is the natural number following 15 and preceding 17. 16 is a composite number, and a square number, being 42 = 4 × 4. It is the smallest number with exactly five divisors, its proper divisors being , , and ....
, 2222 (number)22 is the natural number following 21 and preceding 23.- In mathematics :Twenty-two is an even composite number, its proper divisors being 1, 2 and 11....
, 3434 (number)34 is the natural number following 33 and preceding 35.-In mathematics:34 is the ninth distinct semiprime and has four divisors including unity and itself. Its neighbors, 33 and 35, also are distinct semiprimes, having four divisors each, and 34 is the smallest number to be surrounded by numbers...
, 3636 (number)36 is the natural number following 35 and preceding 37.- In mathematics :36 is both the square of 6 and a triangular number, making it a square triangular number...
, 4646 (number)46 is the natural number following 45 and preceding 47.- In mathematics :Forty-six is a Wedderburn-Etherington number, an enneagonal number and a centered triangular number. It is the sum of the totient function for the first twelve integers. 46 is the largest even integer that can't be expressed...
, 5656 (number)56 is the natural number following 55 and preceding 57.- Mathematics :56 is the sum of the first six triangular numbers , as well as the sum of six consecutive primes . It is also a tetranacci number and a pronic number. Adding up the divisors of 1 through 8 gives 56...
, 6464 (number)64 is the natural number following 63 and preceding 65.-In mathematics:Sixty-four is the square of 8, the cube of 4, and the sixth power of 2. It is the smallest number with exactly seven divisors. It is the lowest positive power of two that is adjacent to neither a Mersenne prime nor a Fermat...
, 6666 (number)66 is the natural number following 65 and preceding 67.Usages of this number include:-Mathematics:*66 is a sphenic number, a triangular number, a hexagonal number, and a semi-meandric number...
, 7070 (number)70 is the natural number following 69 and preceding 71.-In mathematics:Its factorization makes it a sphenic number. 70 is a Pell number and a generalized heptagonal number, one of only two numbers to be both. Also, it is the seventh pentagonal number and the fourth 13-gonal number, as well as the...
… .
(Arguably 0 and 1 could also be included as trivial entries.)
Investigation of such numbers stemmed from a prior conjecture by Paul Erdős
Paul Erdos
Paul Erdős was a Hungarian mathematician. Erdős published more papers than any other mathematician in history, working with hundreds of collaborators. He worked on problems in combinatorics, graph theory, number theory, classical analysis, approximation theory, set theory, and probability theory...
:
- There exists a positive integer k such that every integer a is uniquely determined by the list of prime divisors of
 .
.
Alan R. Woods investigated this for his 1981 thesis, and conjectured that whenever k > 1, the interval
 always included a number coprime
always included a number coprimeCoprime
In number theory, a branch of mathematics, two integers a and b are said to be coprime or relatively prime if the only positive integer that evenly divides both of them is 1. This is the same thing as their greatest common divisor being 1...
to both endpoints. It was only later that he found the first counterexample,
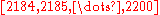 with k = 16.
with k = 16.David L. Dowe proved
Mathematical proof
In mathematics, a proof is a convincing demonstration that some mathematical statement is necessarily true. Proofs are obtained from deductive reasoning, rather than from inductive or empirical arguments. That is, a proof must demonstrate that a statement is true in all cases, without a single...
that there are infinitely many Erdős–Woods numbers, and Cégielski, Heroult and Richard showed that the set is recursive.

