Erdős distinct distances problem
Encyclopedia
In discrete geometry
, the Erdős distinct distances problem states that between distinct points on a plane there are at least distinct distances. It was posed by Paul Erdős
in 1946. In a 2010 preprint, Larry Guth
and Nets Hawk Katz announced a solution.
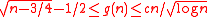for some constant 
. The lower bound was given by an easy argument, the upper bound is given by a 
square grid (as there are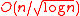 
numbers below n which are sums of two squares, see Landau–Ramanujan constant). Erdős conjectured that the upper bound was closer to the true value of g(n), specifically, 
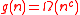holds for every .
, 1952), (Fan Chung
, 1984), (Fan Chung
, Endre Szemerédi
, W. T. Trotter, 1992), (László Székely, 1993), (József Solymosi, C. D. Tóth, 2001), (Gábor Tardos
, 2003), and (Nets Hawk Katz, Gábor Tardos
, 2004).
obtained the lower bound.
Discrete geometry
Discrete geometry and combinatorial geometry are branches of geometry that study combinatorial properties and constructive methods of discrete geometric objects. Most questions in discrete geometry involve finite or discrete sets of basic geometric objects, such as points, lines, planes, circles,...
, the Erdős distinct distances problem states that between distinct points on a plane there are at least distinct distances. It was posed by Paul Erdős
Paul Erdos
Paul Erdős was a Hungarian mathematician. Erdős published more papers than any other mathematician in history, working with hundreds of collaborators. He worked on problems in combinatorics, graph theory, number theory, classical analysis, approximation theory, set theory, and probability theory...
in 1946. In a 2010 preprint, Larry Guth
Larry Guth
Lawrence David Guth is professor of mathematics at the Courant Institute.Guth received his Ph.D. in 2005 from the Massachusetts Institute of Technology under the supervision of Tomasz Mrowka. He won an Alfred P. Sloan Fellowship in . He also was invited speaker at the International Congress of...
and Nets Hawk Katz announced a solution.
The conjecture
In what follows let denote the minimal number of distinct distances between points in the plane. In his 1946 paper, Erdős proved the estimates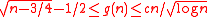 for some constant . The lower bound was given by an easy argument, the upper bound is given by a square grid (as there are 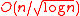numbers below n which are sums of two squares, see Landau–Ramanujan constant). Erdős conjectured that the upper bound was closer to the true value of g(n), specifically, 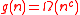holds for every .Partial results
Paul Erdős' 1946 lower bound of was successively improved to: (Leo MoserLeo Moser
Leo Moser was an Austrian-Canadian mathematician, best known for his polygon notation....
, 1952), (Fan Chung
Fan Chung
Fan Rong K Chung Graham , known professionally as Fan Chung, is a mathematician who works mainly in the areas of spectral graph theory, extremal graph theory and random graphs, in particular...
, 1984), (Fan Chung
Fan Chung
Fan Rong K Chung Graham , known professionally as Fan Chung, is a mathematician who works mainly in the areas of spectral graph theory, extremal graph theory and random graphs, in particular...
, Endre Szemerédi
Endre Szemerédi
Endre Szemerédi is a Hungarian mathematician, working in the field of combinatorics and theoretical computer science. He is the State of New Jersey Professor of computer science at Rutgers University since 1986...
, W. T. Trotter, 1992), (László Székely, 1993), (József Solymosi, C. D. Tóth, 2001), (Gábor Tardos
Gábor Tardos
Gábor Tardos is a Hungarian mathematician, currently a professor and Canada Research Chair at Simon Fraser University. He works mainly in combinatorics and computer science...
, 2003), and (Nets Hawk Katz, Gábor Tardos
Gábor Tardos
Gábor Tardos is a Hungarian mathematician, currently a professor and Canada Research Chair at Simon Fraser University. He works mainly in combinatorics and computer science...
, 2004).
Higher dimensions
Erdős also considered the higher dimensional variant of the problem: for d≥3 let gd(n) denote the minimal possible number of distinct distances among n point in the d-dimensional Euclidean space. He proved that and and conjectured that the upper bound is in fact sharp, i.e., . In 2008, Solymosi and VuVan H. Vu
Van H. Vu is a Vietnamese mathematician, a professor of mathematics at Yale University and the 2008 winner of the Pólya Prize of the Society for Industrial and Applied Mathematics for his work on concentration of measure. He is a collaborator of Terence Tao....
obtained the lower bound.
External links
- William Gasarch's page on the problem
- János PachJános PachJános Pach is a mathematician and computer scientist working in the fields of combinatorics and discrete and computational geometry...
's guest post on Gil KalaiGil KalaiGil Kalai is the Henry and Manya Noskwith Professor of Mathematics at the Hebrew University of Jerusalem, and adjunct professor of mathematics and of computer science at Yale University, and the editor of the Israel Journal of Mathematics.-Biography:...
's blog - Terry TaoTerence TaoTerence Chi-Shen Tao FRS is an Australian mathematician working primarily on harmonic analysis, partial differential equations, combinatorics, analytic number theory and representation theory...
's blog entry on the Guth-Katz proof, gives a detailed exposition of the proof.