Error analysis
Encyclopedia
Error analysis is the study of kind and quantity of error
that occurs, particularly in the fields of applied mathematics
(particularly numerical analysis
), applied linguistics
and statistics
.
about a mean
.
For instance, in a system modeled as a function of two variables
. Error analysis deals with the propagation of the numerical error
s in
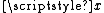and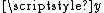 
(around mean values 
and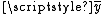 
) to error in 
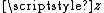(around a mean 
).
In numerical analysis, error analysis comprises both forward error analysis and backward error analysis. Forward error analysis involves the analysis of a function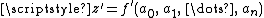
which is an approximation (usually a finite polynomial) to a function 
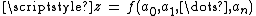to determine the bounds on the error in the approximation; i.e., to find 
such that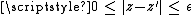 
. Backward error analysis involves the analysis of the approximation function 
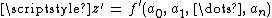, to determine the bounds on the parameters 
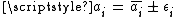such that the result 
.
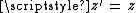, error analysis studies the types and causes of language errors
. Errors are classified according to:
Error analysis in SLA was established in the 1960s by Stephen Pit Corder and colleagues. Error analysis was an alternative to contrastive analysis
, an approach influenced by behaviorism
through which applied linguists sought to use the formal distinctions between the learners' first and second languages to predict errors. Error analysis showed that contrastive analysis was unable to predict a great majority of errors, although its more valuable aspects have been incorporated into the study of language transfer. A key finding of error analysis has been that many learner errors are produced by learners making faulty inferences about the rules of the new language.
(MD) simulations, there are errors due to inadequate sampling of the phase space or infrequently occurring events, these lead to the statistical error due to random fluctuation in the measurements.
For a series of M measurements of a fluctuating property A, the mean value is:
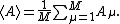
When these M measurements are independent, the variance of the mean <A> is:
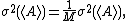
but in most MD simulations, there is correlation between quantity A at different time, so the variance of the mean <A> will be underestimated as the effective number of independent measurements is actually less than M. In such situations we rewrite the variance as :
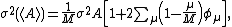
where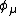
is the autocorrelation function defined by
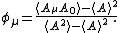
We can then use the autocorrelation function to estimate the error bar
. Luckily, we have a much simpler method based on block averaging.
Error
The word error entails different meanings and usages relative to how it is conceptually applied. The concrete meaning of the Latin word "error" is "wandering" or "straying". Unlike an illusion, an error or a mistake can sometimes be dispelled through knowledge...
that occurs, particularly in the fields of applied mathematics
Applied mathematics
Applied mathematics is a branch of mathematics that concerns itself with mathematical methods that are typically used in science, engineering, business, and industry. Thus, "applied mathematics" is a mathematical science with specialized knowledge...
(particularly numerical analysis
Numerical analysis
Numerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis ....
), applied linguistics
Applied linguistics
Applied linguistics is an interdisciplinary field of study that identifies, investigates, and offers solutions to language-related real-life problems...
and statistics
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
.
Error analysis in numerical modeling
In numerical simulation or modeling of real systems, error analysis is concerned with the changes in the output of the model as the parameters to the model varyVariance
In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
about a mean
Mean
In statistics, mean has two related meanings:* the arithmetic mean .* the expected value of a random variable, which is also called the population mean....
.
For instance, in a system modeled as a function of two variables
. Error analysis deals with the propagation of the numerical errorNumerical error
In software engineering and mathematics, numerical error is the combined effect of two kinds of error in a calculation. The first is caused by the finite precision of computations involving floating-point or integer values...
s in
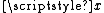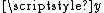and (around mean values and 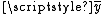) to error in 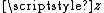(around a mean ).In numerical analysis, error analysis comprises both forward error analysis and backward error analysis. Forward error analysis involves the analysis of a function
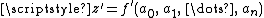which is an approximation (usually a finite polynomial) to a function 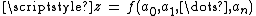to determine the bounds on the error in the approximation; i.e., to find such that 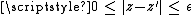. Backward error analysis involves the analysis of the approximation function 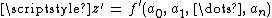, to determine the bounds on the parameters 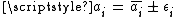such that the result 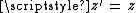.Error analysis in second language acquisition
In second language acquisitionSecond language acquisition
Second-language acquisition or second-language learning is the process by which people learn a second language. Second-language acquisition is also the name of the scientific discipline devoted to studying that process...
, error analysis studies the types and causes of language errors
Speech error
Speech errors, commonly referred to as slips of the tongue , are conscious or unconscious deviations from the apparently intended form of an utterance. They can be subdivided into spontaneously and inadvertently produced speech errors and intentionally produced word-plays or puns...
. Errors are classified according to:
- modality (i.e., level of proficiency in speaking, writingWritingWriting is the representation of language in a textual medium through the use of a set of signs or symbols . It is distinguished from illustration, such as cave drawing and painting, and non-symbolic preservation of language via non-textual media, such as magnetic tape audio.Writing most likely...
, readingReading (process)Reading is a complex cognitive process of decoding symbols for the intention of constructing or deriving meaning . It is a means of language acquisition, of communication, and of sharing information and ideas...
, listening) - linguistic levels (i.e., pronunciationPronunciationPronunciation refers to the way a word or a language is spoken, or the manner in which someone utters a word. If one is said to have "correct pronunciation", then it refers to both within a particular dialect....
, grammarGrammarIn linguistics, grammar is the set of structural rules that govern the composition of clauses, phrases, and words in any given natural language. The term refers also to the study of such rules, and this field includes morphology, syntax, and phonology, often complemented by phonetics, semantics,...
, vocabularyVocabularyA person's vocabulary is the set of words within a language that are familiar to that person. A vocabulary usually develops with age, and serves as a useful and fundamental tool for communication and acquiring knowledge...
, styleStyle (fiction)In fiction, style is the manner in which the author tells the story. Along with plot, character, theme, and setting, style is considered one of the fundamental components of fiction.-Fiction-writing modes:...
) - form (e.g., omission, insertion, substitution)
- type (systematic errors/errors in competence vs. occasional errors/errors in performance)
- cause (e.g., interference, interlanguageInterlanguageAn interlanguage is an emerging linguistic system that has been developed by a learner of a second language who has not become fully proficient yet but is approximating the target language: preserving some features of their first language , or overgeneralizing target language rules in speaking or...
) - norm vs. system
Error analysis in SLA was established in the 1960s by Stephen Pit Corder and colleagues. Error analysis was an alternative to contrastive analysis
Contrastive analysis
Contrastive analysis is the systematic study of a pair of languages with a view to identifying their structural differences and similarities. Historically it has been used to establish language genealogies....
, an approach influenced by behaviorism
Behaviorism
Behaviorism , also called the learning perspective , is a philosophy of psychology based on the proposition that all things that organisms do—including acting, thinking, and feeling—can and should be regarded as behaviors, and that psychological disorders are best treated by altering behavior...
through which applied linguists sought to use the formal distinctions between the learners' first and second languages to predict errors. Error analysis showed that contrastive analysis was unable to predict a great majority of errors, although its more valuable aspects have been incorporated into the study of language transfer. A key finding of error analysis has been that many learner errors are produced by learners making faulty inferences about the rules of the new language.
Error analysis in molecular dynamics simulation
In molecular dynamicsMolecular dynamics
Molecular dynamics is a computer simulation of physical movements of atoms and molecules. The atoms and molecules are allowed to interact for a period of time, giving a view of the motion of the atoms...
(MD) simulations, there are errors due to inadequate sampling of the phase space or infrequently occurring events, these lead to the statistical error due to random fluctuation in the measurements.
For a series of M measurements of a fluctuating property A, the mean value is:
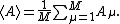
When these M measurements are independent, the variance of the mean <A> is:
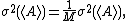
but in most MD simulations, there is correlation between quantity A at different time, so the variance of the mean <A> will be underestimated as the effective number of independent measurements is actually less than M. In such situations we rewrite the variance as :
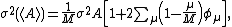
where
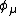is the autocorrelation function defined by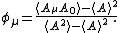We can then use the autocorrelation function to estimate the error bar
Error bar
Error bars are a graphical representation of the variability of data and are used on graphs to indicate the error, or uncertainty in a reported measurement. They give a general idea of how accurate a measurement is, or conversely, how far from the reported value the true value might be...
. Luckily, we have a much simpler method based on block averaging.
See also
- Error barError barError bars are a graphical representation of the variability of data and are used on graphs to indicate the error, or uncertainty in a reported measurement. They give a general idea of how accurate a measurement is, or conversely, how far from the reported value the true value might be...
- Errors and residuals in statisticsErrors and residuals in statisticsIn statistics and optimization, statistical errors and residuals are two closely related and easily confused measures of the deviation of a sample from its "theoretical value"...
- For error analysis in applied linguisticsApplied linguisticsApplied linguistics is an interdisciplinary field of study that identifies, investigates, and offers solutions to language-related real-life problems...
, see contrastive analysisContrastive analysisContrastive analysis is the systematic study of a pair of languages with a view to identifying their structural differences and similarities. Historically it has been used to establish language genealogies.... - Propagation of uncertaintyPropagation of uncertaintyIn statistics, propagation of error is the effect of variables' uncertainties on the uncertainty of a function based on them...
External links
- http://www.physics.arizona.edu/~restrepo/475A/Notes/sourcea/node13.html – Definitions and graphical explanation.
- http://teacher.pas.rochester.edu/PHY_LABS/AppendixB/AppendixB.html All about it.