Properties

• Every Euclidean field is an ordered Pythagorean field
  Pythagorean field
  In algebra, a Pythagorean field is a field in which every sum of two squares is a square. A Pythagorean extension of a field F is an extension obtained by adjoining an element for some λ in F. So a Pythagorean field is one closed under taking Pythagorean extensions...
  
  , but the converse is not true.

Examples

• The real number
  Real number
  In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
  
  s R with the usual operations and ordering form a Euclidean field.
• The field of real algebraic numbers 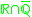is a Euclidean field.
• The field of hyperreal number
  Hyperreal number
  The system of hyperreal numbers represents a rigorous method of treating the infinite and infinitesimal quantities. The hyperreals, or nonstandard reals, *R, are an extension of the real numbers R that contains numbers greater than anything of the form1 + 1 + \cdots + 1. \, Such a number is...
  
  s is an Euclidean field.

Counterexamples

• The rational number
  Rational number
  In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
  
  s Q with the usual operations and ordering do not form a Euclidean field. For example, 2 is not a square in Q since the square root of 2
  Square root of 2
  The square root of 2, often known as root 2, is the positive algebraic number that, when multiplied by itself, gives the number 2. It is more precisely called the principal square root of 2, to distinguish it from the negative number with the same property.Geometrically the square root of 2 is the...
  
   is irrational
  Irrational number
  In mathematics, an irrational number is any real number that cannot be expressed as a ratio a/b, where a and b are integers, with b non-zero, and is therefore not a rational number....
  
  .
• The complex number
  Complex number
  A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
  
  s C do not form a Euclidean field since they cannot be given the structure of an ordered field.