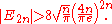Euler number
Encyclopedia
In the area of number theory
, the Euler numbers are a sequence
En of integer
s defined by the following Taylor series
expansion:
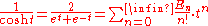
where cosh t is the hyperbolic cosine
. The Euler numbers appear as a special value of the Euler polynomials.
The odd-indexed Euler numbers are all zero
. The even-indexed ones have alternating signs. Some values are:
Some authors re-index the sequence in order to omit the odd-numbered Euler numbers with value zero, and/or change all signs to positive. This encyclopedia adheres to the convention adopted above.
The Euler numbers appear in the Taylor series
expansions of the secant
and hyperbolic secant functions. The latter is the function in the definition. They also occur in combinatorics
; see alternating permutation.
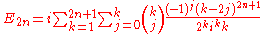
The Euler number E2n can be expressed as a sum over the even partitions
of 2n,
as well as as a sum over the odd partitions of 2n-1,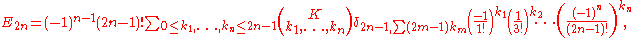
where in both cases and
and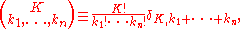
is a multinomial coefficient. The Kronecker delta's restrict the sums over the ks to and to
and to
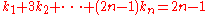 , respectively. As an example,
, respectively. As an example,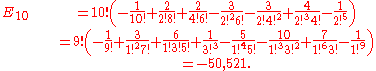
E2n is also given by the determinant
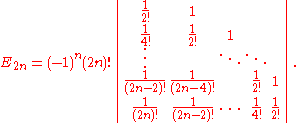
they have the following lower bound
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, the Euler numbers are a sequence
Sequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
En of integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s defined by the following Taylor series
Taylor series
In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
expansion:
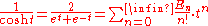
where cosh t is the hyperbolic cosine
Hyperbolic function
In mathematics, hyperbolic functions are analogs of the ordinary trigonometric, or circular, functions. The basic hyperbolic functions are the hyperbolic sine "sinh" , and the hyperbolic cosine "cosh" , from which are derived the hyperbolic tangent "tanh" and so on.Just as the points form a...
. The Euler numbers appear as a special value of the Euler polynomials.
The odd-indexed Euler numbers are all zero
0 (number)
0 is both a numberand the numerical digit used to represent that number in numerals.It fulfills a central role in mathematics as the additive identity of the integers, real numbers, and many other algebraic structures. As a digit, 0 is used as a placeholder in place value systems...
. The even-indexed ones have alternating signs. Some values are:
- E0 = 1
- E2 = −1
- E4 = 5
- E6 = −61
- E8 = 1,385
- E10 = −50,521
- E12 = 2,702,765
- E14 = −199,360,981
- E16 = 19,391,512,145
- E18 = −2,404,879,675,441
Some authors re-index the sequence in order to omit the odd-numbered Euler numbers with value zero, and/or change all signs to positive. This encyclopedia adheres to the convention adopted above.
The Euler numbers appear in the Taylor series
Taylor series
In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
expansions of the secant
Trigonometric function
In mathematics, the trigonometric functions are functions of an angle. They are used to relate the angles of a triangle to the lengths of the sides of a triangle...
and hyperbolic secant functions. The latter is the function in the definition. They also occur in combinatorics
Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
; see alternating permutation.
Explicit formulas
An explicit formula for Euler numbers is given by: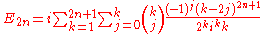
The Euler number E2n can be expressed as a sum over the even partitions
Partition (number theory)
In number theory and combinatorics, a partition of a positive integer n, also called an integer partition, is a way of writing n as a sum of positive integers. Two sums that differ only in the order of their summands are considered to be the same partition; if order matters then the sum becomes a...
of 2n,

as well as as a sum over the odd partitions of 2n-1,
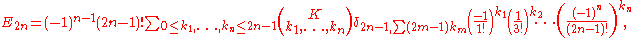
where in both cases
 and
and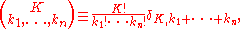
is a multinomial coefficient. The Kronecker delta's restrict the sums over the ks to
 and to
and to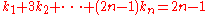 , respectively. As an example,
, respectively. As an example,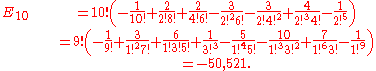
E2n is also given by the determinant
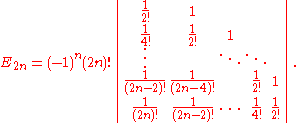
Asymptotic approximation
The Euler numbers grow quite rapidly for large indices asthey have the following lower bound