Euler system
Encyclopedia
In mathematics
, an Euler system is collection of compatible elements of Galois cohomology groups indexed by fields. They were introduced by in his work on Heegner point
s on modular elliptic curve
s, which was motivated by his earlier paper and the work of . Euler systems are named after Leonhard Euler
because the factors relating different elements of an Euler system resemble the Euler factors of an Euler product
.
Euler systems can be used to construct annihilators of ideal class group
s or Selmer groups, thus giving bounds on their orders, which in turn has led to deep theorems such as the finiteness of some Tate-Shafarevich groups. This led to Karl Rubin
's new proof of the main conjecture of Iwasawa theory, considered simpler than the original proof due to Barry Mazur
and Andrew Wiles
.
Kazuya Kato
refers to the elements in an Euler system as "arithmetic incarnations of zeta" and describes the property of being an Euler system as "an arithmetic reflection of the fact that these incarnations are related to special values of Euler products".
αn = 1 − ζn. These satisfy the relations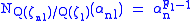
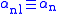modulo all primes above l
where l is a prime not dividing n and Fl is a Frobenius automorphism with Fl(ζn) = ζ.
Kolyvagin used this Euler system to give an elementary proof of the Gras conjecture
.
s of an elliptic curve, and used this to show that in some cases the Tate-Shafarevich group is finite.
of modular curve
s. These elements—named Beilinson elements after Alexander Beilinson
who introduced them in —were used by Kazuya Kato in to prove one divisibility in Barry Mazur's main conjecture of Iwasawa theory for elliptic curve
s.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, an Euler system is collection of compatible elements of Galois cohomology groups indexed by fields. They were introduced by in his work on Heegner point
Heegner point
In mathematics, a Heegner point is a point on a modular elliptic curve that is the image of a quadratic imaginary point of the upper half-plane. They were defined by Bryan Birch and named after Kurt Heegner, who used similar ideas to prove Gauss's conjecture on imaginary quadratic fields of class...
s on modular elliptic curve
Modular elliptic curve
A modular elliptic curve is an elliptic curve E that admits a parametrisation X0 → E by a modular curve. This is not the same as a modular curve that happens to be an elliptic curve, and which could be called an elliptic modular curve...
s, which was motivated by his earlier paper and the work of . Euler systems are named after Leonhard Euler
Leonhard Euler
Leonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...
because the factors relating different elements of an Euler system resemble the Euler factors of an Euler product
Euler product
In number theory, an Euler product is an expansion of a Dirichlet series into an infinite product indexed by prime numbers. The name arose from the case of the Riemann zeta-function, where such a product representation was proved by Leonhard Euler.-Definition:...
.
Euler systems can be used to construct annihilators of ideal class group
Ideal class group
In mathematics, the extent to which unique factorization fails in the ring of integers of an algebraic number field can be described by a certain group known as an ideal class group...
s or Selmer groups, thus giving bounds on their orders, which in turn has led to deep theorems such as the finiteness of some Tate-Shafarevich groups. This led to Karl Rubin
Karl Rubin
Karl Rubin is an American mathematician at University of California, Irvine as Thorp Professor of Mathematics. His research interest is in elliptic curves. He was the first mathematician to show that some elliptic curves over the rationals have finite Tate-Shafarevich groups...
's new proof of the main conjecture of Iwasawa theory, considered simpler than the original proof due to Barry Mazur
Barry Mazur
-Life:Born in New York City, Mazur attended the Bronx High School of Science and MIT, although he did not graduate from the latter on account of failing a then-present ROTC requirement. Regardless, he was accepted for graduate school and received his Ph.D. from Princeton University in 1959,...
and Andrew Wiles
Andrew Wiles
Sir Andrew John Wiles KBE FRS is a British mathematician and a Royal Society Research Professor at Oxford University, specializing in number theory...
.
Definition
Although there are several definitions of special sorts of Euler system, there seems to be no published definition of an Euler system that covers all known cases. But it is possible to say roughly what an Euler system is, as follows:- An Euler system is given by collection of elements cF. These elements are often indexed by certain number fields F containing some fixed number field K, or by something closely related such as square-free integers. The elements cF are typically elements of some Galois cohomology group such as H1(F, T) where T is a p-adic representation of the absolute Galois group of K.
- The most important condition is that the elements cF and cGfor two different fields F ⊆ G are related by a simple formula, such as
- Here the "Euler factor" P(τ|B;x) is defined to be the element det(1-τx|B) considered as an element of O[x], which when x happens to act on B is not the same as det(1-τx|B) considered as an element of O.
- There may be other conditions that the cF have to satisfy, such as congruence conditions.
Kazuya Kato
Kazuya Kato
is a Japanese mathematician. He grew up in the prefecture of Wakayama in Japan. He attended college at the University of Tokyo, from which he also obtained his master's degree in 1975, and his PhD in 1980. He was a professor at Tokyo University, Tokyo Institute of Technology and Kyoto University...
refers to the elements in an Euler system as "arithmetic incarnations of zeta" and describes the property of being an Euler system as "an arithmetic reflection of the fact that these incarnations are related to special values of Euler products".
Cyclotomic units
For every square-free positive integer n pick an n-th root ζn of 1, with ζmn = ζmζn for m,n coprime. Then the cyclotomic Euler system is the set of numbersαn = 1 − ζn. These satisfy the relations
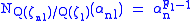
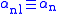modulo all primes above lwhere l is a prime not dividing n and Fl is a Frobenius automorphism with Fl(ζn) = ζ.
Kolyvagin used this Euler system to give an elementary proof of the Gras conjecture
Gras conjecture
In algebraic number theory, the Gras conjecture relates the p-parts of the Galois eigenspaces of an ideal class group to the group of global units modulo cyclotomic units. It was proved by as a corollary of their work on the main conjecture of Iwasawa theory. later gave a simpler proof using...
.
Heegner points
Kolyvagin constructed an Euler system from the Heegner pointHeegner point
In mathematics, a Heegner point is a point on a modular elliptic curve that is the image of a quadratic imaginary point of the upper half-plane. They were defined by Bryan Birch and named after Kurt Heegner, who used similar ideas to prove Gauss's conjecture on imaginary quadratic fields of class...
s of an elliptic curve, and used this to show that in some cases the Tate-Shafarevich group is finite.
Kato's Euler system
Kato's Euler system consists of certain elements occurring in the algebraic K-theoryAlgebraic K-theory
In mathematics, algebraic K-theory is an important part of homological algebra concerned with defining and applying a sequenceof functors from rings to abelian groups, for all integers n....
of modular curve
Modular curve
In number theory and algebraic geometry, a modular curve Y is a Riemann surface, or the corresponding algebraic curve, constructed as a quotient of the complex upper half-plane H by the action of a congruence subgroup Γ of the modular group of integral 2×2 matrices SL...
s. These elements—named Beilinson elements after Alexander Beilinson
Alexander Beilinson
Alexander A. Beilinson is the David and Mary Winton Green University Professor at the University of Chicago and works on mathematics. His research has spanned representation theory, algebraic geometry and mathematical physics...
who introduced them in —were used by Kazuya Kato in to prove one divisibility in Barry Mazur's main conjecture of Iwasawa theory for elliptic curve
Elliptic curve
In mathematics, an elliptic curve is a smooth, projective algebraic curve of genus one, on which there is a specified point O. An elliptic curve is in fact an abelian variety — that is, it has a multiplication defined algebraically with respect to which it is a group — and O serves as the identity...
s.
External links
- Several papers on Kolyvagin systems are available at Barry Mazur's web page (as of July 2005).