In combinatorics

Combinatorics

Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...

 the Eulerian number A(n, m), is the number of permutation

Permutation

In mathematics, the notion of permutation is used with several slightly different meanings, all related to the act of permuting objects or values. Informally, a permutation of a set of objects is an arrangement of those objects into a particular order...

s of the numbers 1 to n in which exactly m elements are greater than the previous element (permutations with m "ascents"). They are the coefficients of the Eulerian polynomials:
This polynomial appears as the numerator in an expression for the generating function

Generating function

In mathematics, a generating function is a formal power series in one indeterminate, whose coefficients encode information about a sequence of numbers an that is indexed by the natural numbers. Generating functions were first introduced by Abraham de Moivre in 1730, in order to solve the general...

 of the sequence
.

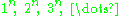Other notations for A(n, m) are E(n, m) and
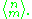
In 1755 Leonhard Euler investigated in his book Institutiones calculi differentialis polynomials α₁(x) = 1, α₂(x) = x + 1, α₃(x) = x² + 4x + 1, etc.