Examples of generating functions
Encyclopedia
The following examples are in the spirit of George Pólya
, who advocated learning mathematics by doing and re-capitulating as many examples and proofs as possible. The purpose of this article is to present common tricks of the trade in context, so that people may incorporate them into their knowledge.
, starting with
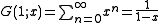
and replacing with
with 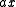 , we obtain
, we obtain
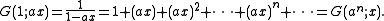
For instance, since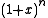 is the generating function for binomial coefficients for a fixed n, one may ask for a bivariate generating function that generates the binomial coefficients
is the generating function for binomial coefficients for a fixed n, one may ask for a bivariate generating function that generates the binomial coefficients 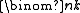 for all k and n.
for all k and n.
To do this, consider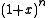 as itself a series (in n), and find the generating function in y that has these as coefficients. Since the generating function for
as itself a series (in n), and find the generating function in y that has these as coefficients. Since the generating function for 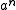 is just
is just 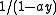 , the generating function for the binomial coefficients is:
, the generating function for the binomial coefficients is: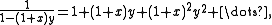
and the coefficient on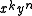 is the
is the 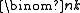 binomial coefficient.
binomial coefficient.
for the Fibonacci number
s Fn defined by F0 = 0, F1 = 1, and Fn = Fn−1 + Fn−2 for n ≥ 2. We form the ordinary generating function

for this sequence. The generating function for the sequence (Fn−1) is xf and that of (Fn−2) is x2f. From the recurrence relation, we therefore see that the power series xf + x2f agrees with f except for the first two coefficients:
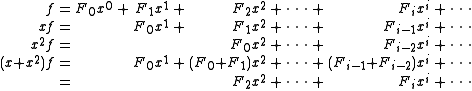
Taking these into account, we find that
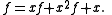
(This is the crucial step; recurrence relations can almost always be translated into equations for the generating functions.) Solving this equation for f, we get
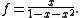
The denominator can be factored using the golden ratio
φ1 = (1 + √5)/2 and φ2 = (1 − √5)/2, and the technique of partial fraction decomposition yields
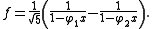
These two formal power series are known explicitly because they are geometric series; comparing coefficients, we find the explicit formula
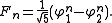
George Pólya
George Pólya was a Hungarian mathematician. He was a professor of mathematics from 1914 to 1940 at ETH Zürich and from 1940 to 1953 at Stanford University. He made fundamental contributions to combinatorics, number theory, numerical analysis and probability theory...
, who advocated learning mathematics by doing and re-capitulating as many examples and proofs as possible. The purpose of this article is to present common tricks of the trade in context, so that people may incorporate them into their knowledge.
Worked example A: basics
New generating functions can be created by extending simpler generating functions. For exampleWorked-example effect
The worked-example effect is a learning effect predicted by cognitive load theory . According to Sweller: "The worked example effect is the best known and most widely studied of the cognitive load effects"The worked-example effect is a learning effect predicted by cognitive load theory (Sweller,...
, starting with
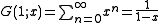
and replacing
 with
with 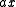 , we obtain
, we obtain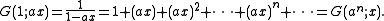
Bivariate generating functions
One can define generating functions in several variables, for series with several indices. These are often called super generating functions, and for 2 variables are often called bivariate generating functions.For instance, since
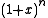 is the generating function for binomial coefficients for a fixed n, one may ask for a bivariate generating function that generates the binomial coefficients
is the generating function for binomial coefficients for a fixed n, one may ask for a bivariate generating function that generates the binomial coefficients 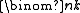 for all k and n.
for all k and n.To do this, consider
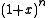 as itself a series (in n), and find the generating function in y that has these as coefficients. Since the generating function for
as itself a series (in n), and find the generating function in y that has these as coefficients. Since the generating function for 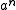 is just
is just 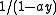 , the generating function for the binomial coefficients is:
, the generating function for the binomial coefficients is: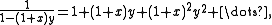
and the coefficient on
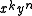 is the
is the 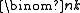 binomial coefficient.
binomial coefficient.Worked example B: Fibonacci numbers
Consider the problem of finding a closed formulaClosed-form expression
In mathematics, an expression is said to be a closed-form expression if it can be expressed analytically in terms of a bounded number of certain "well-known" functions...
for the Fibonacci number
Fibonacci number
In mathematics, the Fibonacci numbers are the numbers in the following integer sequence:0,\;1,\;1,\;2,\;3,\;5,\;8,\;13,\;21,\;34,\;55,\;89,\;144,\; \ldots\; ....
s Fn defined by F0 = 0, F1 = 1, and Fn = Fn−1 + Fn−2 for n ≥ 2. We form the ordinary generating function

for this sequence. The generating function for the sequence (Fn−1) is xf and that of (Fn−2) is x2f. From the recurrence relation, we therefore see that the power series xf + x2f agrees with f except for the first two coefficients:
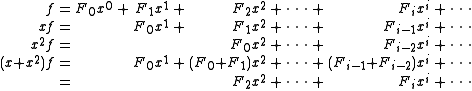
Taking these into account, we find that
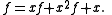
(This is the crucial step; recurrence relations can almost always be translated into equations for the generating functions.) Solving this equation for f, we get
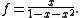
The denominator can be factored using the golden ratio
Golden ratio
In mathematics and the arts, two quantities are in the golden ratio if the ratio of the sum of the quantities to the larger quantity is equal to the ratio of the larger quantity to the smaller one. The golden ratio is an irrational mathematical constant, approximately 1.61803398874989...
φ1 = (1 + √5)/2 and φ2 = (1 − √5)/2, and the technique of partial fraction decomposition yields
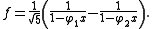
These two formal power series are known explicitly because they are geometric series; comparing coefficients, we find the explicit formula
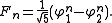
External links
- Generating Functions, Power Indices and Coin Change at cut-the-knotCut-the-knotCut-the-knot is a free, advertisement-funded educational website maintained by Alexander Bogomolny and devoted to popular exposition of many topics in mathematics. The site has won more than 20 awards from scientific and educational publications, including a Scientific American Web Award in 2003,...
- Generatingfunctionology (PDF)

