Exhaustion by compact sets
Encyclopedia
In mathematics
, especially analysis
, exhaustion by compact sets of an open set
E in the Euclidean space
Rn (or a manifold
with countable base) is an increasing sequence
of compact sets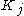
, where by increasing we mean 
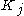is a subset
of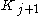
, with the limit (union) of the sequence being E.
Sometimes one requires the sequence of compact sets to satisfy one more property— that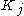
is contained in the interior
of
for each 
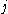. This, however, is dispensed in Rn or a manifold with countable base.
For example, consider a unit open disk and the concentric closed disk of each radius inside. That is let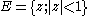
and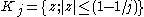 
. Then taking the limit (union) of the sequence 
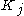gives E. The example can be easily generalized in other dimensions.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, especially analysis
Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
, exhaustion by compact sets of an open set
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
E in the Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
Rn (or a manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
with countable base) is an increasing sequence
Sequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
of compact sets
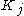, where by increasing we mean 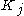is a subsetSubset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
of
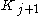, with the limit (union) of the sequence being E.Sometimes one requires the sequence of compact sets to satisfy one more property— that
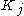is contained in the interiorInterior (topology)
In mathematics, specifically in topology, the interior of a set S of points of a topological space consists of all points of S that do not belong to the boundary of S. A point that is in the interior of S is an interior point of S....
of
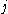for each . This, however, is dispensed in Rn or a manifold with countable base.For example, consider a unit open disk and the concentric closed disk of each radius inside. That is let
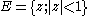and 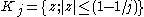. Then taking the limit (union) of the sequence 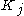gives E. The example can be easily generalized in other dimensions.