
Exponentiated weibull distribution
Encyclopedia
In statistics
, the exponentiated Weibull family of probability distribution
s was introduced by Mudholkar and Srivastava (1993) as an extension of the Weibull family obtained by adding a second shape parameter
.
The cumulative distribution function
for the exponentiated Weibull distribution is
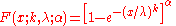
for x ≥ 0, and F(x; k; λ; α) = 0 for x < 0. Here k > 0 is the first shape parameter
, α > 0 is the second shape parameter and λ > 0 is the scale parameter
of the distribution.
There are two important special cases:
* and monotone
failure rate
s. A similar distribution was introduced in 1984 by Zacks, called a Weibull-exponential distribution (Zacks 1984). Mudholkar, Srivastava, and Kollia (1996) applied the generalized Weibull distribution to model survival data. They showed that the distribution has increasing, decreasing, bathtub, and unimodal hazard functions. Mudholkar, Srivastava, and Freimer (1995), Mudholkar and Hutson (1996) and Nassar and Eissa (2003) studied various properties of the exponentiated Weibull distribution. Mudholkar et al. (1995) applied the exponentiated Weibull distribution to model failure data. Mudholkar and Hutson (1996) applied the exponentiated Weibull distribution to extreme value data. They showed that the exponentiated Weibull distribution has increasing, decreasing, bathtub, and unimodal hazard rates. The exponentiated exponential distribution
proposed by Gupta and Kundu (1999, 2001) is a special case of the exponentiated Weibull family. Later, the moments of the EW distribution were derived by Choudhury (2005). Also, M. Pal, M.M. Ali, J. Woo (2006) studied the EW distribution and compared it with the two-parameter Weibull and gamma distributions with respect to failure rate.
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, the exponentiated Weibull family of probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
s was introduced by Mudholkar and Srivastava (1993) as an extension of the Weibull family obtained by adding a second shape parameter
Shape parameter
In probability theory and statistics, a shape parameter is a kind of numerical parameter of a parametric family of probability distributions.- Definition :...
.
The cumulative distribution function
Cumulative distribution function
In probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...
for the exponentiated Weibull distribution is
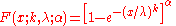
for x ≥ 0, and F(x; k; λ; α) = 0 for x < 0. Here k > 0 is the first shape parameter
Shape parameter
In probability theory and statistics, a shape parameter is a kind of numerical parameter of a parametric family of probability distributions.- Definition :...
, α > 0 is the second shape parameter and λ > 0 is the scale parameter
Scale parameter
In probability theory and statistics, a scale parameter is a special kind of numerical parameter of a parametric family of probability distributions...
of the distribution.
There are two important special cases:
- α = 1 gives the Weibull distribution;
- k = 1 gives the exponentiated exponential distribution.
Background
The family of distributions accommodates unimodal, bathtub shapedBathtub curve
The bathtub curve is widely used in reliability engineering. It describes a particular form of the hazard function which comprises three parts:*The first part is a decreasing failure rate, known as early failures....
* and monotone
Monotonic function
In mathematics, a monotonic function is a function that preserves the given order. This concept first arose in calculus, and was later generalized to the more abstract setting of order theory....
failure rate
Failure rate
Failure rate is the frequency with which an engineered system or component fails, expressed for example in failures per hour. It is often denoted by the Greek letter λ and is important in reliability engineering....
s. A similar distribution was introduced in 1984 by Zacks, called a Weibull-exponential distribution (Zacks 1984). Mudholkar, Srivastava, and Kollia (1996) applied the generalized Weibull distribution to model survival data. They showed that the distribution has increasing, decreasing, bathtub, and unimodal hazard functions. Mudholkar, Srivastava, and Freimer (1995), Mudholkar and Hutson (1996) and Nassar and Eissa (2003) studied various properties of the exponentiated Weibull distribution. Mudholkar et al. (1995) applied the exponentiated Weibull distribution to model failure data. Mudholkar and Hutson (1996) applied the exponentiated Weibull distribution to extreme value data. They showed that the exponentiated Weibull distribution has increasing, decreasing, bathtub, and unimodal hazard rates. The exponentiated exponential distribution
Exponential distribution
In probability theory and statistics, the exponential distribution is a family of continuous probability distributions. It describes the time between events in a Poisson process, i.e...
proposed by Gupta and Kundu (1999, 2001) is a special case of the exponentiated Weibull family. Later, the moments of the EW distribution were derived by Choudhury (2005). Also, M. Pal, M.M. Ali, J. Woo (2006) studied the EW distribution and compared it with the two-parameter Weibull and gamma distributions with respect to failure rate.

