Exterior angle theorem
Encyclopedia
The exterior angle theorem can mean one of two things: Postulate 1.16 in Euclid's Elements
which states that the exterior angle of a triangle
is bigger than either of the remote interior angles, or a theorem
in elementary geometry which states that the exterior angle of a triangle is equal to the sum of the two remote interior angles.
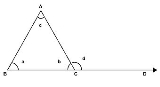
A triangle has three corners, called vertices. The sides of a triangle that come together at a vertex form an angle. This angle is called the interior angle. In the picture below, the angles a, b and c are the three interior angles of the triangle. An exterior angle is formed by extending one of the sides of the triangle; the angle between the extended side and the other side is the exterior angle. In the picture, angle d is an exterior angle.
The exterior angle theorem says that the size of an exterior angle at a vertex of a triangle equals the sum of the sizes of the interior angles at the other two vertices of the triangle. So, in the picture, the size of angle d equals the size of angle a plus the size of angle c.
To prove: m ACD = m
ACD = m ABC + m
ABC + m BAC (here, m
BAC (here, m ACD denotes the size of the angle ACD)
ACD denotes the size of the angle ACD)
Proof:
Hence, proved.
Euclid's Elements
Euclid's Elements is a mathematical and geometric treatise consisting of 13 books written by the Greek mathematician Euclid in Alexandria c. 300 BC. It is a collection of definitions, postulates , propositions , and mathematical proofs of the propositions...
which states that the exterior angle of a triangle
Triangle
A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....
is bigger than either of the remote interior angles, or a theorem
Theorem
In mathematics, a theorem is a statement that has been proven on the basis of previously established statements, such as other theorems, and previously accepted statements, such as axioms...
in elementary geometry which states that the exterior angle of a triangle is equal to the sum of the two remote interior angles.
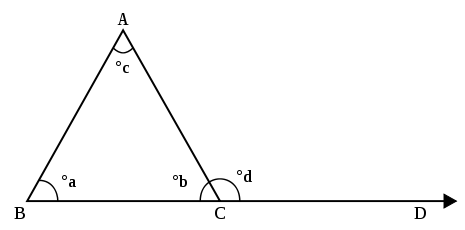
A triangle has three corners, called vertices. The sides of a triangle that come together at a vertex form an angle. This angle is called the interior angle. In the picture below, the angles a, b and c are the three interior angles of the triangle. An exterior angle is formed by extending one of the sides of the triangle; the angle between the extended side and the other side is the exterior angle. In the picture, angle d is an exterior angle.
The exterior angle theorem says that the size of an exterior angle at a vertex of a triangle equals the sum of the sizes of the interior angles at the other two vertices of the triangle. So, in the picture, the size of angle d equals the size of angle a plus the size of angle c.

Proof
Given: In ∆ABC, angle ACD is the exterior angle.To prove: m
 ACD = m
ACD = m ABC + m
ABC + m BAC (here, m
BAC (here, m ACD denotes the size of the angle ACD)
ACD denotes the size of the angle ACD)Proof:
| Statements | Reason |
|---|---|
In ∆ABC, m a + m a + m b + m b + m c = 180°------[1] c = 180°------[1] |
Sum of the measures of all the angles of a triangle is 180° |
Also, m b + m b + m d = 180°-------[2] d = 180°-------[2] |
Linear pair axiom |
m a + m a + m c + m c + m b = m b = m b + m b + m d d |
Transitive Property of Equality |
m a + m a + m c + c +  b b b b d d |
Addition Property of Equality (also known as Subtraction Property of Equality) |
∴ m d = m d = m a + m a + m c c |
|
i.e. m ACD = m ACD = m ABC + m ABC + m BAC BAC |
Hence, proved.

