Extra element theorem
Encyclopedia
The Extra Element Theorem (EET) is an analytic technique developed by R.D. Middlebrook for simplifying the process of deriving driving point and transfer function
s for linear electronic circuits. Much like Thevenin's theorem
, the extra element theorem breaks down one complicated problem into several simpler ones.
Driving point and transfer functions can generally be found using KVL and KCL methods, however several complicated equations may result that offer little insight into the circuit's behavior. Using the extra element theorem, a circuit element (such as a resistor
) can be removed from a circuit and the desired driving point or transfer function found. By removing the element that most complicates the circuit (such as an element that creates feedback
), the desired function can be easier to obtain. Next two correctional factors must be found and combined with the previously derived function to find the exact expression.
The general form of the extra element theorem is called the N-extra element theorem and allows multiple circuit elements to be removed at once.
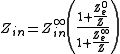
where
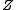is the impedance chosen as the extra element
is the input impedance with Z removed (or made infinite)
is the impedance seen by the extra element Z with the input shorted (or made zero)
is the impedance seen by the extra element Z with the input open (or made infinite)
Computing these three terms may seem like extra effort, but they are often easier to compute than the overall input impedance.
for the circuit in Figure 1 using the EET (note all component values are unity for simplicity). If the capacitor (gray shading) is denoted the extra element then
Removing this capacitor from the circuit we find
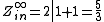
Calculating the impedance seen by the capacitor with the input shorted we find
Calculating the impedance seen by the capacitor with the input open we find
Therefore using the EET, we find
Note that this problem was solved by calculating three simple driving point impedances by inspection.
Transfer function
A transfer function is a mathematical representation, in terms of spatial or temporal frequency, of the relation between the input and output of a linear time-invariant system. With optical imaging devices, for example, it is the Fourier transform of the point spread function i.e...
s for linear electronic circuits. Much like Thevenin's theorem
Thévenin's theorem
In circuit theory, Thévenin's theorem for linear electrical networks states that any combination of voltage sources, current sources, and resistors with two terminals is electrically equivalent to a single voltage source V and a single series resistor R. For single frequency AC systems the theorem...
, the extra element theorem breaks down one complicated problem into several simpler ones.
Driving point and transfer functions can generally be found using KVL and KCL methods, however several complicated equations may result that offer little insight into the circuit's behavior. Using the extra element theorem, a circuit element (such as a resistor
Resistor
A linear resistor is a linear, passive two-terminal electrical component that implements electrical resistance as a circuit element.The current through a resistor is in direct proportion to the voltage across the resistor's terminals. Thus, the ratio of the voltage applied across a resistor's...
) can be removed from a circuit and the desired driving point or transfer function found. By removing the element that most complicates the circuit (such as an element that creates feedback
Feedback
Feedback describes the situation when output from an event or phenomenon in the past will influence an occurrence or occurrences of the same Feedback describes the situation when output from (or information about the result of) an event or phenomenon in the past will influence an occurrence or...
), the desired function can be easier to obtain. Next two correctional factors must be found and combined with the previously derived function to find the exact expression.
The general form of the extra element theorem is called the N-extra element theorem and allows multiple circuit elements to be removed at once.
Driving point impedances
As a special case, the EET can be used to find the input impedance of a network. For this application the EET can be written as: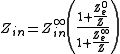where
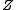is the impedance chosen as the extra element is the input impedance with Z removed (or made infinite) is the impedance seen by the extra element Z with the input shorted (or made zero) is the impedance seen by the extra element Z with the input open (or made infinite)Computing these three terms may seem like extra effort, but they are often easier to compute than the overall input impedance.
Example
Consider the problem of finding for the circuit in Figure 1 using the EET (note all component values are unity for simplicity). If the capacitor (gray shading) is denoted the extra element thenRemoving this capacitor from the circuit we find
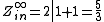
Calculating the impedance seen by the capacitor with the input shorted we find
Calculating the impedance seen by the capacitor with the input open we find
Therefore using the EET, we find
Note that this problem was solved by calculating three simple driving point impedances by inspection.