Fallacy of the undistributed middle
Encyclopedia
The fallacy of the undistributed middle is a logical fallacy, and more specifically a formal fallacy
, that is committed when the middle term
in a categorical syllogism is not distributed in the major premise. It is thus a syllogistic fallacy
.
The fallacy of the undistributed middle occurs when the term that links the two premises is never distributed.
In this example, distribution is marked in boldface:
B is the common term between the two premises (the middle term) but is never distributed, so this syllogism is invalid.
Also, a related rule of logic is that anything distributed in the conclusion must be distributed in at least one premise.
The middle term - Z - is distributed, but Y is distributed in the conclusion and not in any premise, so this syllogism is invalid.
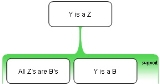
This can be graphically represented as follows:

where the premises are in the green box and the conclusion is indicated above them.
Here, B is the middle term, and it is not distributed in the major premise, "all Zs are Bs".
It may or may not be the case that "all Zs are Bs," but this is irrelevant to the conclusion. What is relevant to the conclusion is whether it is true that "all Bs are Zs," which is ignored in the argument. The fallacy is similar to affirming the consequent
and denying the antecedent
. However, the fallacy may be resolved if the terms are exchanged in either the conclusion or in the first co-premise
. Indeed, from the perspective of first-order logic
, all cases of the fallacy of the undistributed middle are, in fact, examples of affirming the consequent or denying the antecedent, depending on the structure of the fallacious argument.

The middle term is the one that appears in both premise
s — in this case, it is the class of backpack carriers. It is undistributed because neither of its uses applies to all backpack carriers. Therefore it can't be used to connect students and my grandfather — both of them could be separate and unconnected divisions of the class of backpack carriers. Note below how "carries a backpack" is truly undistributed:
Specifically, the structure of this example results in affirming the consequent
.
However, if the latter two statements were switched, the syllogism would be valid:
In this case, the middle term is the class of students, and the first use clearly refers to 'all students'. It is therefore distributed across the whole of its class, and so can be used to connect the other two terms (backpack carriers, and my grandfather). Again, note below that "student" is distributed:
Formal fallacy
In philosophy, a formal fallacy is a pattern of reasoning that is always wrong. This is due to a flaw in the logical structure of the argument which renders the argument invalid...
, that is committed when the middle term
Middle term
The middle term must distributed in at least one premises but not in the conclusion of a categorical syllogism. The major term and the minor terms, also called the end terms, do appear in the conclusion.Example:...
in a categorical syllogism is not distributed in the major premise. It is thus a syllogistic fallacy
Syllogistic fallacy
Syllogistic fallacies are logical fallacies that occur in syllogisms. They include:Any syllogism type :*fallacy of four termsOccurring in categorical syllogisms:*related to affirmative or negative premises:...
.
Classical Formulation
In classical syllogisms, all statements consist of two terms and are in the form of "A" (all), "E" (none), "I" (some), or "O" (some not). The first term is distributed in A statements; the second is distributed in O statements; both are distributed in E statements; and none are distributed in I statements.The fallacy of the undistributed middle occurs when the term that links the two premises is never distributed.
In this example, distribution is marked in boldface:
- All Zs are Bs
- (All) y is a B
- Therefore
- (All) y is a Z
B is the common term between the two premises (the middle term) but is never distributed, so this syllogism is invalid.
Also, a related rule of logic is that anything distributed in the conclusion must be distributed in at least one premise.
- All Zs are Bs
- Some Ys are Zs
- Therefore
- All Ys are Bs
The middle term - Z - is distributed, but Y is distributed in the conclusion and not in any premise, so this syllogism is invalid.
Pattern
The fallacy of the undistributed middle takes the following form:- All Zs are Bs
- Y is a B
- Therefore, Y is a Z
This can be graphically represented as follows:

where the premises are in the green box and the conclusion is indicated above them.
Here, B is the middle term, and it is not distributed in the major premise, "all Zs are Bs".
It may or may not be the case that "all Zs are Bs," but this is irrelevant to the conclusion. What is relevant to the conclusion is whether it is true that "all Bs are Zs," which is ignored in the argument. The fallacy is similar to affirming the consequent
Affirming the consequent
Affirming the consequent, sometimes called converse error, is a formal fallacy, committed by reasoning in the form:#If P, then Q.#Q.#Therefore, P....
and denying the antecedent
Denying the antecedent
Denying the antecedent, sometimes also called inverse error, is a formal fallacy, committed by reasoning in the form:The name denying the antecedent derives from the premise "not P", which denies the "if" clause of the conditional premise....
. However, the fallacy may be resolved if the terms are exchanged in either the conclusion or in the first co-premise
Co-premise
A co-premise is a premise in reasoning and informal logic which is not the main supporting reason for a contention or a lemma, but is logically necessary to ensure the validity of an argument...
. Indeed, from the perspective of first-order logic
First-order logic
First-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic...
, all cases of the fallacy of the undistributed middle are, in fact, examples of affirming the consequent or denying the antecedent, depending on the structure of the fallacious argument.
Examples
For example:- All students carry backpacks.
- My grandfather carries a backpack.
- Therefore, my grandfather is a student.
- All students carry backpacks.
- My grandfather carries a backpack.
- Everyone who carries a backpack is a student.
- Therefore, my grandfather is a student.

The middle term is the one that appears in both premise
Premise
Premise can refer to:* Premise, a claim that is a reason for, or an objection against, some other claim as part of an argument...
s — in this case, it is the class of backpack carriers. It is undistributed because neither of its uses applies to all backpack carriers. Therefore it can't be used to connect students and my grandfather — both of them could be separate and unconnected divisions of the class of backpack carriers. Note below how "carries a backpack" is truly undistributed:
- grandfather is someone who carries a backpack; student is someone who carries a backpack
Specifically, the structure of this example results in affirming the consequent
Affirming the consequent
Affirming the consequent, sometimes called converse error, is a formal fallacy, committed by reasoning in the form:#If P, then Q.#Q.#Therefore, P....
.
However, if the latter two statements were switched, the syllogism would be valid:
- All students carry backpacks.
- My grandfather is a student.
- Therefore, my grandfather carries a backpack.
In this case, the middle term is the class of students, and the first use clearly refers to 'all students'. It is therefore distributed across the whole of its class, and so can be used to connect the other two terms (backpack carriers, and my grandfather). Again, note below that "student" is distributed:
- grandfather is a student and thus carries a backpack
External links
- Undistributed Middle entry in The Fallacy Files

