Farkas's lemma
Encyclopedia
Farkas' lemma is a result in mathematics
stating that a vector is either in a given convex cone
or that there exists a (hyper)plane
separating the vector from the cone, but not both. It was originally proved by the Hungarian mathematician Gyula Farkas
. It is used amongst other things in the proof of the Karush–Kuhn–Tucker theorem in nonlinear programming
.
Farkas' lemma is an example of a theorem of the alternative; a theorem stating that of two systems, one or the other has a solution, but not both or none.
and b an m-dimensional vector
. Then, exactly one of the following two statements is true:
Here, the notation x ≥ 0 means that all components of the vector x are nonnegative.
There are a number of slightly different (but equivalent) formulations of the Lemma in the literature. The one given here is due to Gale
, Kuhn and Tucker
in 1951.
The vectors x1a1 + ··· + xnan with nonnegative coefficients constitute the convex cone
of the set {a1, …, an} so the first statement says that b is in this cone.
The second statement says that there exists a vector y such that the angle of y with the vectors ai is at most 90° while the angle of y with the vector b is more than 90°. The hyperplane normal to this vector has the vectors ai on one side and the vector b on the other side. Hence, this hyperplane separates the vectors in the cone of {a1, …, an} and the vector b.
For example, let n,m=2 and a1 = (1,0)T and a2 = (1,1)T. The convex cone spanned by a1 and a2 can be seen as a wedge-shaped slice of the first quadrant in the x-y plane. Now, suppose b = (0,1). Certainly, b is not in the convex cone a1x1+a2x2. Hence, there must be a separating hyperplane. Let y = (1,−1)T. We can see that a1 · y = 1, a2 · y = 0, and b · y = −1. Hence, the hyperplane with normal y indeed separates the convex cone a1x1+a2x2 from b.
Farkas' lemma can thus be interpreted geometrically as follows: Given a convex cone and a vector, either the vector is in the cone or there is a hyperplane separating the vector from the cone, but not both.
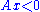has a solution x, or 
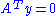has a nonzero solution y with y ≥ 0.
A particularly suggestive and easy-to-remember version is the following: if a set of inequalities has no solution, then a contradiction can be produced from it by linear combination with nonnegative coefficients. In formulas: if
≤ 
is unsolvable then 
, 
,
≥ 
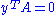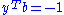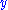has a solution. (Note that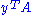 
is a combination of the left hand sides, 
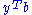a combination of the right hand side of the inequalities. Since the positive combination produces a zero vector on the left and a −1 on the right, the contradiction is apparent.)
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
stating that a vector is either in a given convex cone
Cone (linear algebra)
In linear algebra, a cone is a subset of a vector space that is closed under multiplication by positive scalars. In other words, a subset C of a real vector space V is a cone if and only if λx belongs to C for any x in C and any positive scalar λ of V .A cone is said...
or that there exists a (hyper)plane
Hyperplane
A hyperplane is a concept in geometry. It is a generalization of the plane into a different number of dimensions.A hyperplane of an n-dimensional space is a flat subset with dimension n − 1...
separating the vector from the cone, but not both. It was originally proved by the Hungarian mathematician Gyula Farkas
Gyula Farkas (natural scientist)
Farkas Gyula, or Julius Farkas was a Hungarian mathematician and physicist.He attended the gymnasium at Győr , and studied law and philosophy at Budapest...
. It is used amongst other things in the proof of the Karush–Kuhn–Tucker theorem in nonlinear programming
Nonlinear programming
In mathematics, nonlinear programming is the process of solving a system of equalities and inequalities, collectively termed constraints, over a set of unknown real variables, along with an objective function to be maximized or minimized, where some of the constraints or the objective function are...
.
Farkas' lemma is an example of a theorem of the alternative; a theorem stating that of two systems, one or the other has a solution, but not both or none.
Statement of the lemma
Let A be an m × n matrixMatrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
and b an m-dimensional vector
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
. Then, exactly one of the following two statements is true:
- There exists an x ∈ Rn such that Ax = b and x ≥ 0.
- There exists a y ∈ Rm such that ATy ≥ 0 and bTy < 0.
Here, the notation x ≥ 0 means that all components of the vector x are nonnegative.
There are a number of slightly different (but equivalent) formulations of the Lemma in the literature. The one given here is due to Gale
David Gale
David Gale was a distinguished American mathematician and economist. He was a Professor Emeritus at University of California, Berkeley, affiliated with departments of Mathematics, Economics, and Industrial Engineering and Operations Research...
, Kuhn and Tucker
Albert W. Tucker
Albert William Tucker was a Canadian-born American mathematician who made important contributions in topology, game theory, and non-linear programming....
in 1951.
Geometric interpretation
Let a1, …, an ∈ Rm denote the columns of A. In terms of these vectors, Farkas' lemma states that exactly one of the following two statements is true:- There exist non-negative coefficients x1, …, xn ∈ R such that b = x1a1 + ··· + xnan.
- There exists a vector y ∈ Rm such that ai · y ≥ 0 for i = 1, …, n and b · y < 0.
The vectors x1a1 + ··· + xnan with nonnegative coefficients constitute the convex cone
Convex cone
In linear algebra, a convex cone is a subset of a vector space over an ordered field that is closed under linear combinations with positive coefficients.-Definition:...
of the set {a1, …, an} so the first statement says that b is in this cone.
The second statement says that there exists a vector y such that the angle of y with the vectors ai is at most 90° while the angle of y with the vector b is more than 90°. The hyperplane normal to this vector has the vectors ai on one side and the vector b on the other side. Hence, this hyperplane separates the vectors in the cone of {a1, …, an} and the vector b.
For example, let n,m=2 and a1 = (1,0)T and a2 = (1,1)T. The convex cone spanned by a1 and a2 can be seen as a wedge-shaped slice of the first quadrant in the x-y plane. Now, suppose b = (0,1). Certainly, b is not in the convex cone a1x1+a2x2. Hence, there must be a separating hyperplane. Let y = (1,−1)T. We can see that a1 · y = 1, a2 · y = 0, and b · y = −1. Hence, the hyperplane with normal y indeed separates the convex cone a1x1+a2x2 from b.
Farkas' lemma can thus be interpreted geometrically as follows: Given a convex cone and a vector, either the vector is in the cone or there is a hyperplane separating the vector from the cone, but not both.
Further implications
Farkas' lemma can be varied to many further theorems of alternative by simple modifications, such as Gordan's theorem: Either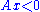 has a solution x, or 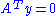has a nonzero solution y with y ≥ 0.A particularly suggestive and easy-to-remember version is the following: if a set of inequalities has no solution, then a contradiction can be produced from it by linear combination with nonnegative coefficients. In formulas: if
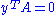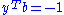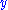≤ is unsolvable then , , ≥ has a solution. (Note that 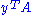is a combination of the left hand sides, 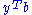a combination of the right hand side of the inequalities. Since the positive combination produces a zero vector on the left and a −1 on the right, the contradiction is apparent.)