
Fejér's theorem
Encyclopedia
In mathematics, Fejér's theorem, named for Hungarian
mathematician
Lipót Fejér
, states that if f:R → C is a continuous function
with period
2π, then the sequence
(σn) of Cesàro means of the sequence (sn) of partial sums of the Fourier series
of f converges uniformly to f on [-π,π].
Explicitly,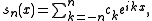
where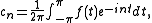
and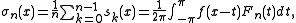
with Fn being the nth order Fejér kernel.
A more general form of the theorem applies to functions which are not necessarily continuous . Suppose that f is in L1(-π,π). If the left and right limits f(x0±0) of f(x) exist at x0, or if both limits are infinite of the same sign, then
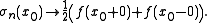
Existence or divergence to infinity of the Cesàro mean is also implied. By a theorem of Marcel Riesz
, Fejér's theorem holds precisely as stated if the (C, 1) mean σn is replaced with (C, α) mean
of the Fourier series .
Hungary
Hungary , officially the Republic of Hungary , is a landlocked country in Central Europe. It is situated in the Carpathian Basin and is bordered by Slovakia to the north, Ukraine and Romania to the east, Serbia and Croatia to the south, Slovenia to the southwest and Austria to the west. The...
mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
Lipót Fejér
Lipót Fejér
Lipót Fejér , was a Hungarian mathematician. Fejér was born Leopold Weiss, and changed to the Hungarian name Fejér around 1900....
, states that if f:R → C is a continuous function
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
with period
Periodic function
In mathematics, a periodic function is a function that repeats its values in regular intervals or periods. The most important examples are the trigonometric functions, which repeat over intervals of length 2π radians. Periodic functions are used throughout science to describe oscillations,...
2π, then the sequence
Sequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
(σn) of Cesàro means of the sequence (sn) of partial sums of the Fourier series
Fourier series
In mathematics, a Fourier series decomposes periodic functions or periodic signals into the sum of a set of simple oscillating functions, namely sines and cosines...
of f converges uniformly to f on [-π,π].
Explicitly,
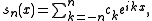
where
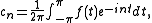
and
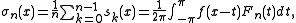
with Fn being the nth order Fejér kernel.
A more general form of the theorem applies to functions which are not necessarily continuous . Suppose that f is in L1(-π,π). If the left and right limits f(x0±0) of f(x) exist at x0, or if both limits are infinite of the same sign, then
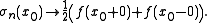
Existence or divergence to infinity of the Cesàro mean is also implied. By a theorem of Marcel Riesz
Marcel Riesz
Marcel Riesz was a Hungarian mathematician who was born in Győr, Hungary . He moved to Sweden in 1908 and spent the rest of his life there, dying in Lund, where he was a professor from 1926 at Lund University...
, Fejér's theorem holds precisely as stated if the (C, 1) mean σn is replaced with (C, α) mean
Cesàro summation
In mathematical analysis, Cesàro summation is an alternative means of assigning a sum to an infinite series. If the series converges in the usual sense to a sum A, then the series is also Cesàro summable and has Cesàro sum A...
of the Fourier series .

