Finite Fourier transform
Encyclopedia
In mathematics
the finite Fourier transform may refer to either
or
or
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
the finite Fourier transform may refer to either
- another name for the discrete Fourier transformDiscrete Fourier transformIn mathematics, the discrete Fourier transform is a specific kind of discrete transform, used in Fourier analysis. It transforms one function into another, which is called the frequency domain representation, or simply the DFT, of the original function...
or
- another name for the Fourier seriesFourier seriesIn mathematics, a Fourier series decomposes periodic functions or periodic signals into the sum of a set of simple oscillating functions, namely sines and cosines...
coefficients
or
- a transform based on a Fourier-transform-like integral applied to a function
, but with integration only on a finite interval, usually taken to be the interval 
. Equivalently, it is the Fourier transformFourier transformIn mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
of a function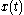
multiplied by a rectangular window functionWindow functionIn signal processing, a window function is a mathematical function that is zero-valued outside of some chosen interval. For instance, a function that is constant inside the interval and zero elsewhere is called a rectangular window, which describes the shape of its graphical representation...
. That is, the finite Fourier transform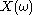
of a function 
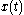on the finite interval 
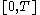is given by: