Finite intersection property
Encyclopedia
In general topology
, a branch of mathematics, the finite intersection property is a property of a collection of subsets of a set X. A collection has this property if the intersection over any finite subcollection of the collection is nonempty.
A centered system of sets is a collection of sets with the finite intersection property.
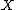be a set with 
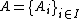a family of subsets of 
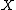. Then the collection 
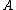has the finite intersection property (fip), if any finite subcollection 
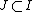has non-empty intersection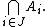 
by inclusion (equivalently, for any finite subcollection, a particular element of the subcollection is contained in all the other elements of the subcollection), e.g. the nested sequence of intervals
.
These are not the only possibilities however. For example, if X = (0, 1) and for each positive integer i, Xi is the set of elements of X having a decimal expansion with digit 0 in the ith decimal place, then any finite intersection is nonempty (just take 0 in those finitely many places and 1 in the rest), but the intersection of all Xi for i≥1 is empty, since no element of (0, 1) has all zero digits.
The finite intersection property is useful in formulating an alternative definition of compactness
: a space is compact if and only if every collection of closed sets satisfying the finite intersection property has nonempty intersection itself. This formulation of compactness is used in some proofs of Tychonoff's theorem
and the uncountability
of the real number
s (see next section)
Let X be a compact
Hausdorff space
that satisfies the property that no one-point set is open. If X has more than one point, then X is uncountable.
Before proving this, we give some examples:
1. We cannot eliminate the Hausdorff condition; a countable set with the indiscrete topology is compact, has more than one point, and satisfies the property that no one point sets are open, but is not uncountable.
2. We cannot eliminate the compactness condition as the set of all rational numbers shows.
3. We cannot eliminate the condition that one point sets cannot be open as a finite space given the discrete topology shows.
Proof of theorem:
Let X be a compact Hausdorff space. We will show that if U is a nonempty, open
subset of X and if x is a point of X, then there is a neighbourhood
V contained in U whose closure
doesn’t contain x (x may or may not be in U). First of all, choose y in U different from x (if x is in U, then there must exist such a y for otherwise U would be an open one point set; if x isn’t in U, this is possible since U is nonempty). Then by the Hausdorff condition, choose disjoint neighbourhoods W and K of x and y respectively. Then (K ∩ U) will be a neighbourhood of y contained in U whose closure doesn’t contain x as desired.
Now suppose ƒ is a bijective function from Z (the positive integers) to X. Denote the points of the image of Z under ƒ as {x1, x2, ……}. Let X be the first open set and choose a neighbourhood U1 contained in X whose closure doesn’t contain x1. Secondly, choose a neighbourhood U2 contained in U1 whose closure doesn’t contain x2. Continue this process whereby choosing a neighbourhood Un+1 contained in Un whose closure doesn’t contain xn+1. Note that the collection {Ui} for i in the positive integers satisfies the finite intersection property and hence the intersection of their closures is nonempty (by the compactness of X). Therefore there is a point x in this intersection. No xi can belong to this intersection because xi doesn’t belong to the closure of Ui. This means that x is not equal to xi for all i and ƒ is not surjective; a contradiction. Therefore, X is uncountable.
Corollary
Every closed interval [a, b] (a < b) is uncountable. Therefore, the set of real numbers is uncountable.
Corollary
Every locally compact
Hausdorff space that is also perfect
is uncountable.
Proof
Suppose X is a locally compact Hausdorff space that is perfect and compact. Then it immediately follows that X is uncountable (from the theorem). If X is a locally compact Hausdorff, perfect space that is not compact, then the one-point compactification of X is a compact Hausdorff space that is also perfect. It follows that the one point compactification of X is uncountable. Therefore X is uncountable (deleting a point from an uncountable set still retains the uncountability of that set).
, 
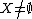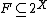, F having the finite intersection property. Then there exists an 
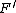ultrafilter
(in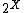
) such that 
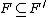. See details and proof in . This result is known as ultrafilter lemma.
General topology
In mathematics, general topology or point-set topology is the branch of topology which studies properties of topological spaces and structures defined on them...
, a branch of mathematics, the finite intersection property is a property of a collection of subsets of a set X. A collection has this property if the intersection over any finite subcollection of the collection is nonempty.
A centered system of sets is a collection of sets with the finite intersection property.
Definition
Let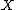 be a set with 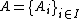a family of subsets of 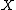. Then the collection 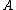has the finite intersection property (fip), if any finite subcollection 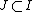has non-empty intersection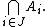 Discussion
Clearly the empty set cannot belong to any collection with the f.i.p. The condition is trivially satisfied if the intersection over the entire collection is nonempty (in particular, if the collection itself is empty), and it is also trivially satisfied if the collection is nested, meaning that the collection is totally orderedTotal order
In set theory, a total order, linear order, simple order, or ordering is a binary relation on some set X. The relation is transitive, antisymmetric, and total...
by inclusion (equivalently, for any finite subcollection, a particular element of the subcollection is contained in all the other elements of the subcollection), e.g. the nested sequence of intervals
.
These are not the only possibilities however. For example, if X = (0, 1) and for each positive integer i, Xi is the set of elements of X having a decimal expansion with digit 0 in the ith decimal place, then any finite intersection is nonempty (just take 0 in those finitely many places and 1 in the rest), but the intersection of all Xi for i≥1 is empty, since no element of (0, 1) has all zero digits.
The finite intersection property is useful in formulating an alternative definition of compactness
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
: a space is compact if and only if every collection of closed sets satisfying the finite intersection property has nonempty intersection itself. This formulation of compactness is used in some proofs of Tychonoff's theorem
Tychonoff's theorem
In mathematics, Tychonoff's theorem states that the product of any collection of compact topological spaces is compact. The theorem is named after Andrey Nikolayevich Tychonoff, who proved it first in 1930 for powers of the closed unit interval and in 1935 stated the full theorem along with the...
and the uncountability
Uncountable set
In mathematics, an uncountable set is an infinite set that contains too many elements to be countable. The uncountability of a set is closely related to its cardinal number: a set is uncountable if its cardinal number is larger than that of the set of all natural numbers.-Characterizations:There...
of the real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s (see next section)
Applications
TheoremLet X be a compact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
Hausdorff space
Hausdorff space
In topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
that satisfies the property that no one-point set is open. If X has more than one point, then X is uncountable.
Before proving this, we give some examples:
1. We cannot eliminate the Hausdorff condition; a countable set with the indiscrete topology is compact, has more than one point, and satisfies the property that no one point sets are open, but is not uncountable.
2. We cannot eliminate the compactness condition as the set of all rational numbers shows.
3. We cannot eliminate the condition that one point sets cannot be open as a finite space given the discrete topology shows.
Proof of theorem:
Let X be a compact Hausdorff space. We will show that if U is a nonempty, open
Open
- Philosophy :* Openness, term being used to define the basis of how various groups and organizations operate- Mathematics :* Open problem, a well-defined problem with no known solution in science and mathematics...
subset of X and if x is a point of X, then there is a neighbourhood
Neighbourhood
A neighbourhood or neighborhood is a geographically localised community within a larger city, town or suburb. Neighbourhoods are often social communities with considerable face-to-face interaction among members. "Researchers have not agreed on an exact definition...
V contained in U whose closure
Closure (topology)
In mathematics, the closure of a subset S in a topological space consists of all points in S plus the limit points of S. Intuitively, these are all the points that are "near" S. A point which is in the closure of S is a point of closure of S...
doesn’t contain x (x may or may not be in U). First of all, choose y in U different from x (if x is in U, then there must exist such a y for otherwise U would be an open one point set; if x isn’t in U, this is possible since U is nonempty). Then by the Hausdorff condition, choose disjoint neighbourhoods W and K of x and y respectively. Then (K ∩ U) will be a neighbourhood of y contained in U whose closure doesn’t contain x as desired.
Now suppose ƒ is a bijective function from Z (the positive integers) to X. Denote the points of the image of Z under ƒ as {x1, x2, ……}. Let X be the first open set and choose a neighbourhood U1 contained in X whose closure doesn’t contain x1. Secondly, choose a neighbourhood U2 contained in U1 whose closure doesn’t contain x2. Continue this process whereby choosing a neighbourhood Un+1 contained in Un whose closure doesn’t contain xn+1. Note that the collection {Ui} for i in the positive integers satisfies the finite intersection property and hence the intersection of their closures is nonempty (by the compactness of X). Therefore there is a point x in this intersection. No xi can belong to this intersection because xi doesn’t belong to the closure of Ui. This means that x is not equal to xi for all i and ƒ is not surjective; a contradiction. Therefore, X is uncountable.
Corollary
Every closed interval [a, b] (a < b) is uncountable. Therefore, the set of real numbers is uncountable.
Corollary
Every locally compact
Locally compact space
In topology and related branches of mathematics, a topological space is called locally compact if, roughly speaking, each small portion of the space looks like a small portion of a compact space.-Formal definition:...
Hausdorff space that is also perfect
Perfect space
In mathematics, in the field of topology, perfect spaces are spaces that have no isolated points. In such spaces, every point can be approximated arbitrarily well by other points - given any point and any topological neighborhood of the point, there is another point within the neighborhood.The...
is uncountable.
Proof
Suppose X is a locally compact Hausdorff space that is perfect and compact. Then it immediately follows that X is uncountable (from the theorem). If X is a locally compact Hausdorff, perfect space that is not compact, then the one-point compactification of X is a compact Hausdorff space that is also perfect. It follows that the one point compactification of X is uncountable. Therefore X is uncountable (deleting a point from an uncountable set still retains the uncountability of that set).
Theorems
Let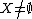, , 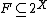F having the finite intersection property. Then there exists an 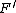ultrafilterUltrafilter
In the mathematical field of set theory, an ultrafilter on a set X is a collection of subsets of X that is a filter, that cannot be enlarged . An ultrafilter may be considered as a finitely additive measure. Then every subset of X is either considered "almost everything" or "almost nothing"...
(in
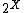) such that 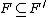. See details and proof in . This result is known as ultrafilter lemma.