
Fitting ideal
Encyclopedia
In commutative algebra
, the Fitting ideals of a finitely generated module over a commutative ring
describe the obstructions to generating the module by a given number of elements. They were introduced by .
with relations
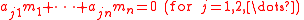
then the ith Fitting ideal Fitti(M) of M is generated by the minors (determinants of submatrices) of order n − i of the matrix ajk.
The Fitting ideals do not depend on the choice of generators and relations of M.
Some authors defined the Fitting ideal I(M) to be the first nonzero Fitting ideal Fitti(M).
If M can be generated by n elements then Fittn(M) = R, and if R is local the converse holds. We have Fitt0(M) ⊆ Ann(M) (the annihilator of M), and Ann(M)Fitti(M) ⊆ Fitti−1(M), so in particular if M can be generated by n elements then Ann(M)n ⊆ Fitt0(M).
If M is a finite abelian group of order |M| (considered as a module over the integers) then the Fitting ideal Fitt0(M) is the ideal (|M|).
The Alexander polynomial
of a knot is a generator of the Fitting ideal of the first homology of the infinite abelian cover of the knot complement.
Commutative algebra
Commutative algebra is the branch of abstract algebra that studies commutative rings, their ideals, and modules over such rings. Both algebraic geometry and algebraic number theory build on commutative algebra...
, the Fitting ideals of a finitely generated module over a commutative ring
Commutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
describe the obstructions to generating the module by a given number of elements. They were introduced by .
Definition
If M is a finitely generated module over a commutative ring R generated by elements m1,...,mnwith relations
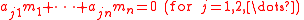
then the ith Fitting ideal Fitti(M) of M is generated by the minors (determinants of submatrices) of order n − i of the matrix ajk.
The Fitting ideals do not depend on the choice of generators and relations of M.
Some authors defined the Fitting ideal I(M) to be the first nonzero Fitting ideal Fitti(M).
Properties
The Fitting ideals are increasing- Fitt0(M) ⊆ Fitt1(M) ⊆ Fitt2(M) ...
If M can be generated by n elements then Fittn(M) = R, and if R is local the converse holds. We have Fitt0(M) ⊆ Ann(M) (the annihilator of M), and Ann(M)Fitti(M) ⊆ Fitti−1(M), so in particular if M can be generated by n elements then Ann(M)n ⊆ Fitt0(M).
Examples
If M is free of rank n then the Fitting ideals Fitti(M) are zero for i<n and R for i ≥ n.If M is a finite abelian group of order |M| (considered as a module over the integers) then the Fitting ideal Fitt0(M) is the ideal (|M|).
The Alexander polynomial
Alexander polynomial
In mathematics, the Alexander polynomial is a knot invariant which assigns a polynomial with integer coefficients to each knot type. James Waddell Alexander II discovered this, the first knot polynomial, in 1923...
of a knot is a generator of the Fitting ideal of the first homology of the infinite abelian cover of the knot complement.

