
Fixed point property
Encyclopedia
A mathematical
object X has the fixed-point property if every suitably well-behaved mapping from X to itself has a fixed point
. It is a special case of the fixed morphism property. The term is most commonly used to describe topological space
s on which every continuous mapping has a fixed point. But another use is in order theory
, where a partially ordered set
P is said to have the fixed point property if every increasing function on P has a fixed point.
C. Then A has the fixed-point property if every morphism
(i.e., every function
)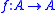 has a fixed point.
has a fixed point.
The most common usage is when C=Top is the category of topological spaces. Then a topological space X has the fixed-point property if every continuous map has a fixed point.
has a fixed point.
, there is some point x0 with g(x0) = 0, which is to say that f(x0) − x0 = 0, and so x0 is a fixed point.
The open interval does not have the fixed-point property. The mapping f(x) = x2 has no fixed point on the interval (0,1).
A of a space X with the fixed-point property also has the fixed-point property. This is because if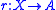 is a retraction and
is a retraction and 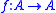 is any continuous function, then the composition
is any continuous function, then the composition  (where
(where  is inclusion) has a fixed point. That is, there is
is inclusion) has a fixed point. That is, there is 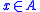 such that
such that 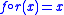 . Since
. Since 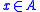 we have that
we have that 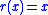 and therefore
and therefore 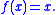
A topological space has the fixed-point property if and only if its identity map is universal.
A product of spaces with the fixed-point property in general fails to have the fixed-point property even if one of the spaces is the closed real interval.
The FPP is a topological invariant, i.e. is preserved by any homeomorphism
. The FPP is also preserved by any retraction
.
According to Brouwer fixed point theorem
every compact
and convex
subset of an euclidean space
has the FPP. Compactness alone does not imply the FPP and convexity is not even a topological property so it makes sense to ask how to topologically characterize the FPP. In 1932 Borsuk
asked whether compactness together with contractibility
could be a necessary and sufficient condition for the FPP to hold. The problem was open for 20 years until the conjecture was disproved by Kinoshita who found an example of a compact contractible space without the FPP.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
object X has the fixed-point property if every suitably well-behaved mapping from X to itself has a fixed point
Fixed point (mathematics)
In mathematics, a fixed point of a function is a point that is mapped to itself by the function. A set of fixed points is sometimes called a fixed set...
. It is a special case of the fixed morphism property. The term is most commonly used to describe topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
s on which every continuous mapping has a fixed point. But another use is in order theory
Order theory
Order theory is a branch of mathematics which investigates our intuitive notion of order using binary relations. It provides a formal framework for describing statements such as "this is less than that" or "this precedes that". This article introduces the field and gives some basic definitions...
, where a partially ordered set
Partially ordered set
In mathematics, especially order theory, a partially ordered set formalizes and generalizes the intuitive concept of an ordering, sequencing, or arrangement of the elements of a set. A poset consists of a set together with a binary relation that indicates that, for certain pairs of elements in the...
P is said to have the fixed point property if every increasing function on P has a fixed point.
Definition
Let A be an object in the concrete categoryConcrete category
In mathematics, a concrete category is a category that is equipped with a faithful functor to the category of sets. This functor makes it possible to think of the objects of the category as sets with additional structure, and of its morphisms as structure-preserving functions...
C. Then A has the fixed-point property if every morphism
Morphism
In mathematics, a morphism is an abstraction derived from structure-preserving mappings between two mathematical structures. The notion of morphism recurs in much of contemporary mathematics...
(i.e., every function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
)
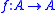 has a fixed point.
has a fixed point.The most common usage is when C=Top is the category of topological spaces. Then a topological space X has the fixed-point property if every continuous map
 has a fixed point.
has a fixed point.The closed interval
The closed interval [0,1] has the fixed point property: Let f:[0,1] → [0,1] be a continuous mapping. If f(0) = 0 or f(1) = 1, then our mapping has a fixed point at 0 or 1. If not, then f(0) > 0 and f(1) − 1 < 0. Thus the function g(x) = f(x) − x is a continuous real valued function which is positive at x = 0 and negative at x = 1. By the intermediate value theoremIntermediate value theorem
In mathematical analysis, the intermediate value theorem states that for each value between the least upper bound and greatest lower bound of the image of a continuous function there is at least one point in its domain that the function maps to that value....
, there is some point x0 with g(x0) = 0, which is to say that f(x0) − x0 = 0, and so x0 is a fixed point.
The open interval does not have the fixed-point property. The mapping f(x) = x2 has no fixed point on the interval (0,1).
The closed disc
The closed interval is a special case of the closed disc, which in any finite dimension has the fixed-point property by the Brouwer fixed-point theorem.Topology
A retractDeformation retract
In topology, a branch of mathematics, a retraction , as the name suggests, "retracts" an entire space into a subspace. A deformation retraction is a map which captures the idea of continuously shrinking a space into a subspace.- Retract :...
A of a space X with the fixed-point property also has the fixed-point property. This is because if
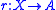 is a retraction and
is a retraction and 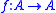 is any continuous function, then the composition
is any continuous function, then the composition  (where
(where  is inclusion) has a fixed point. That is, there is
is inclusion) has a fixed point. That is, there is 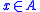 such that
such that 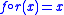 . Since
. Since 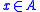 we have that
we have that 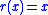 and therefore
and therefore 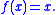
A topological space has the fixed-point property if and only if its identity map is universal.
A product of spaces with the fixed-point property in general fails to have the fixed-point property even if one of the spaces is the closed real interval.
The FPP is a topological invariant, i.e. is preserved by any homeomorphism
Homeomorphism
In the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
. The FPP is also preserved by any retraction
Retraction
A retraction is a public statement, by the author of an earlier statement, that withdraws, cancels, refutes, diametrically reverses the original statement or ceases and desists from publishing the original statement...
.
According to Brouwer fixed point theorem
Brouwer fixed point theorem
Brouwer's fixed-point theorem is a fixed-point theorem in topology, named after Luitzen Brouwer. It states that for any continuous function f with certain properties there is a point x0 such that f = x0. The simplest form of Brouwer's theorem is for continuous functions f from a disk D to...
every compact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
and convex
Convex set
In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...
subset of an euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
has the FPP. Compactness alone does not imply the FPP and convexity is not even a topological property so it makes sense to ask how to topologically characterize the FPP. In 1932 Borsuk
Karol Borsuk
Karol Borsuk was a Polish mathematician.His main interest was topology.Borsuk introduced the theory of absolute retracts and absolute neighborhood retracts , and the cohomotopy groups, later called Borsuk-Spanier cohomotopy groups. He also founded the so called Shape theory...
asked whether compactness together with contractibility
Contractible space
In mathematics, a topological space X is contractible if the identity map on X is null-homotopic, i.e. if it is homotopic to some constant map. Intuitively, a contractible space is one that can be continuously shrunk to a point....
could be a necessary and sufficient condition for the FPP to hold. The problem was open for 20 years until the conjecture was disproved by Kinoshita who found an example of a compact contractible space without the FPP.

