
Flat function
Encyclopedia
In mathematics
, especially real analysis
, a flat function is a smooth function
ƒ : ℝ → ℝ all of whose derivative
s vanish at a given point x0 ∈ ℝ. The flat functions are, in some sense, the antitheses of the analytic function
s. An analytic function ƒ : ℝ → ℝ is given by a convergent power series close to some point x0 ∈ ℝ:
In the case of a flat function we see that all derivatives vanish at x0 ∈ ℝ, i.e. ƒ(k)(x0) = 0 for all k ∈ ℕ. This means that a Taylor series
expansion is impossible; i.e. there is no convergent infinite power series. In the language of Taylor's theorem, the non-constant part of the function always lies in the remainder Rn(x) for all n ∈ ℕ.
Notice that the function need not be flat everywhere. The constant function
s on ℝ are flat functions at all of their points. But there are other, non-trivial, examples.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, especially real analysis
Real analysis
Real analysis, is a branch of mathematical analysis dealing with the set of real numbers and functions of a real variable. In particular, it deals with the analytic properties of real functions and sequences, including convergence and limits of sequences of real numbers, the calculus of the real...
, a flat function is a smooth function
Smooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
ƒ : ℝ → ℝ all of whose derivative
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
s vanish at a given point x0 ∈ ℝ. The flat functions are, in some sense, the antitheses of the analytic function
Analytic function
In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...
s. An analytic function ƒ : ℝ → ℝ is given by a convergent power series close to some point x0 ∈ ℝ:

In the case of a flat function we see that all derivatives vanish at x0 ∈ ℝ, i.e. ƒ(k)(x0) = 0 for all k ∈ ℕ. This means that a Taylor series
Taylor series
In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
expansion is impossible; i.e. there is no convergent infinite power series. In the language of Taylor's theorem, the non-constant part of the function always lies in the remainder Rn(x) for all n ∈ ℕ.
Notice that the function need not be flat everywhere. The constant function
Constant function
In mathematics, a constant function is a function whose values do not vary and thus are constant. For example the function f = 4 is constant since f maps any value to 4...
s on ℝ are flat functions at all of their points. But there are other, non-trivial, examples.
Example
The function defined by-
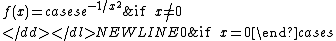
is flat at x = 0.

