Flipped SO(10)
Encyclopedia
Flipped SO is a grand unified theory which is to standard SO(10)
as flipped SU(5)
is to SU(5).
In conventional SO(10) models, the fermions lie in three spinorial 16 representations, one for each generation, which decomposes under [SU(5)× U(1)χ]/Z5 as
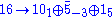
This can either be the Georgi-Glashow SU(5) or flipped SU(5).
In flipped SO(10) models, however, the gauge group is not just SO(10) but SO(10)F×U(1)B or [SO(10)F×U(1)B]/Z4. The fermion fields are now three copies of
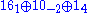
These contain the Standard Model fermions as well as additional vector fermions with GUT scale masses. If we suppose [SU(5)×U(1)A]/Z5 is a subgroup of SO(10)F, then we have the intermediate scale symmetry breaking
where
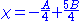
In that case,
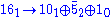
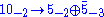
note that the Standard Model fermion fields (including the right handed neutrinos) come from all three [SO(10)F× U(1)B]/Z4 representations. In particular, they happen to be the 101 of 161, the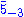
of 10-2 and the 15 of 14 (my apologies for mixing up SO(10)×U(1) notation with SU(5)×U(1) notation, but it would be really cumbersome if we have to spell out which group any given notation happens to refer to. It is left up to the reader to determine the group from the context. This is a standard practice in the GUT model building literature anyway).
The other remaining fermions are vectorlike. To see this, note that with a 161H and a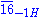
Higgs field, we can have VEVs which breaks the GUT group down to [SU(5)×U(1)χ]/Z4. The Yukawa coupling
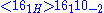
will pair up the 5-2 and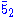
fermions. And we can always introduce a sterile neutrino φ which is invariant under [SO(10)×U(1)B]/Z4 and add the Yukawa coupling
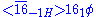
OR we can add the nonrenormalizable term
Either way, the 10 component of the fermion 161 gets taken care of so that it is no longer chiral.
It has been left unspecified so far whether [SU(5)×U(1)χ]/Z5 is the Georgi-Glashow SU(5) or the flipped SU(5). This is because both alternatives lead to reasonable GUT models.
One reason for studying flipped SO(10) is because it can be derived from an E6 GUT model.
SO(10) (physics)
In particle physics, one of the grand unified theories is based on the SO Lie group....
as flipped SU(5)
Flipped SU(5)
The Flipped SU model is a Grand Unified Theory theory first contemplated by Stephen Barr in 1982, and by Dimitri Nanopoulos and others in 1984...
is to SU(5).
In conventional SO(10) models, the fermions lie in three spinorial 16 representations, one for each generation, which decomposes under [SU(5)× U(1)χ]/Z5 as
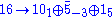
This can either be the Georgi-Glashow SU(5) or flipped SU(5).
In flipped SO(10) models, however, the gauge group is not just SO(10) but SO(10)F×U(1)B or [SO(10)F×U(1)B]/Z4. The fermion fields are now three copies of
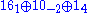
These contain the Standard Model fermions as well as additional vector fermions with GUT scale masses. If we suppose [SU(5)×U(1)A]/Z5 is a subgroup of SO(10)F, then we have the intermediate scale symmetry breaking
where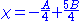In that case,
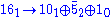
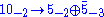
note that the Standard Model fermion fields (including the right handed neutrinos) come from all three [SO(10)F× U(1)B]/Z4 representations. In particular, they happen to be the 101 of 161, the
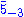of 10-2 and the 15 of 14 (my apologies for mixing up SO(10)×U(1) notation with SU(5)×U(1) notation, but it would be really cumbersome if we have to spell out which group any given notation happens to refer to. It is left up to the reader to determine the group from the context. This is a standard practice in the GUT model building literature anyway).The other remaining fermions are vectorlike. To see this, note that with a 161H and a
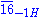Higgs field, we can have VEVs which breaks the GUT group down to [SU(5)×U(1)χ]/Z4. The Yukawa coupling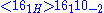will pair up the 5-2 and
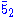fermions. And we can always introduce a sterile neutrino φ which is invariant under [SO(10)×U(1)B]/Z4 and add the Yukawa coupling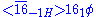OR we can add the nonrenormalizable term
Either way, the 10 component of the fermion 161 gets taken care of so that it is no longer chiral.
It has been left unspecified so far whether [SU(5)×U(1)χ]/Z5 is the Georgi-Glashow SU(5) or the flipped SU(5). This is because both alternatives lead to reasonable GUT models.
One reason for studying flipped SO(10) is because it can be derived from an E6 GUT model.