Floret pentagonal tiling
Encyclopedia
In geometry
, the floret pentagonal tiling is a dual semiregular tiling of the Euclidean plane. It is one of 14 known isohedral pentagon tiling
s. It is given its name because its six pentagonal tiles radiate out from a central point, like petals on a flower
. Conway
calls it a 6-fold pentille.
, and has rotational symmetry of orders 6-3-2 symmetry.
s (V3.3.3.3.n). (The sequence progresses into tilings the hyperbolic plane to any n.) These face-transitive figures have (n32) rotational symmetry.
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, the floret pentagonal tiling is a dual semiregular tiling of the Euclidean plane. It is one of 14 known isohedral pentagon tiling
Pentagon tiling
In geometry, a pentagon tiling is a tiling of the plane by pentagons. A regular pentagonal tiling on the Euclidean plane is impossible because the internal angle of a regular pentagon, 108 is not a divisor of 360...
s. It is given its name because its six pentagonal tiles radiate out from a central point, like petals on a flower
Flower
A flower, sometimes known as a bloom or blossom, is the reproductive structure found in flowering plants . The biological function of a flower is to effect reproduction, usually by providing a mechanism for the union of sperm with eggs...
. Conway
John Horton Conway
John Horton Conway is a prolific mathematician active in the theory of finite groups, knot theory, number theory, combinatorial game theory and coding theory...
calls it a 6-fold pentille.
Dual tiling
It is the dual of the uniform tiling, snub hexagonal tilingSnub hexagonal tiling
In geometry, the Snub hexagonal tiling is a semiregular tiling of the Euclidean plane. There are four triangles and one hexagon on each vertex...
, and has rotational symmetry of orders 6-3-2 symmetry.
Related polyhedra and tilings
This tiling is topologically related as a part of sequence of polyhedra of pentagons with face configurationFace configuration
In geometry, a face configuration is notational description of a face-transitive polyhedron. It represents a sequential count of the number of faces that exist at each vertex around a face....
s (V3.3.3.3.n). (The sequence progresses into tilings the hyperbolic plane to any n.) These face-transitive figures have (n32) rotational symmetry.
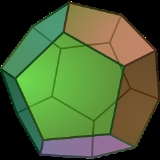
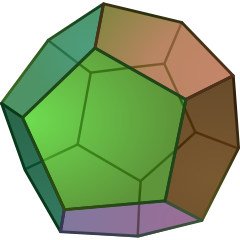 V3.3.3.3.3 (332) and (532) |
 V3.3.3.3.4 Pentagonal icositetrahedron In geometry, a pentagonal icositetrahedron is a Catalan solid which is the dual of the snub cube. It has two distinct forms, which are mirror images of each other.... (432) |
 V3.3.3.3.5 Pentagonal hexecontahedron In geometry, a pentagonal hexecontahedron is a Catalan solid, dual of the snub dodecahedron. It has two distinct forms, which are mirror images of each other. It is also well-known to be the Catalan Solid with the most vertices... (532) |
 V3.3.3.3.6 (632) |
 V3.3.3.3.7 (732) |
External links
- Wolfram alpha floret pentagonal tiling

