Fourier integral operator
Encyclopedia
In mathematical analysis
, Fourier integral operators have become an important tool in the theory of partial differential equations. The class of Fourier integral operators contains differential operator
s as well as classical integral operators as special cases.
A Fourier integral operator T is given by:
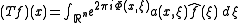
where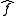
denotes the Fourier transform of f, a(x,ξ) is a standard symbol which is compactly supported in x and Φ is real valued and homogeneous of degree 1 in ξ. It is also necessary to require that 
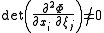on the support of a. Under these conditions, if a is of order zero, it is possible to show that T defines a bounded operator from L2 to L2.
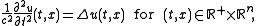
and
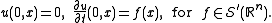
The solution to this problem is given by
These need to be interpreted as oscillatory integrals since they do not in general converge. This formally looks like a sum of two Fourier integral operators, however the coefficients in each of the integrals are not smooth at the origin, and so not standard symbols. If we cut out this singularity with a cutoff function, then the so obtained operators still provide solutions to the initial value problem modulo smooth functions. Thus, if we are only interested in the propagation of singularities of the initial data, it is sufficient to consider such operators. In fact, if we allow the sound speed c in the wave equation to vary with position we can still find a Fourier integral operator that provides a solution modulo smooth functions, and Fourier integral operators thus provide a useful tool for studying the propagation of singularities of solutions to variable speed wave equations, and more generally for other hyperbolic equations.
Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
, Fourier integral operators have become an important tool in the theory of partial differential equations. The class of Fourier integral operators contains differential operator
Differential operator
In mathematics, a differential operator is an operator defined as a function of the differentiation operator. It is helpful, as a matter of notation first, to consider differentiation as an abstract operation, accepting a function and returning another .This article considers only linear operators,...
s as well as classical integral operators as special cases.
A Fourier integral operator T is given by:
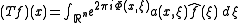
where
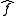denotes the Fourier transform of f, a(x,ξ) is a standard symbol which is compactly supported in x and Φ is real valued and homogeneous of degree 1 in ξ. It is also necessary to require that 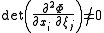on the support of a. Under these conditions, if a is of order zero, it is possible to show that T defines a bounded operator from L2 to L2.Examples
One motivation for the study of Fourier integral operators is the solution operator for the initial value problem for the wave operator. Indeed, consider the following problem: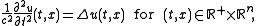and
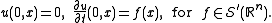
The solution to this problem is given by
These need to be interpreted as oscillatory integrals since they do not in general converge. This formally looks like a sum of two Fourier integral operators, however the coefficients in each of the integrals are not smooth at the origin, and so not standard symbols. If we cut out this singularity with a cutoff function, then the so obtained operators still provide solutions to the initial value problem modulo smooth functions. Thus, if we are only interested in the propagation of singularities of the initial data, it is sufficient to consider such operators. In fact, if we allow the sound speed c in the wave equation to vary with position we can still find a Fourier integral operator that provides a solution modulo smooth functions, and Fourier integral operators thus provide a useful tool for studying the propagation of singularities of solutions to variable speed wave equations, and more generally for other hyperbolic equations.
See also
- Microlocal analysisMicrolocal analysisIn mathematical analysis, microlocal analysis comprises techniques developed from the 1950s onwards based on Fourier transforms related to the study of variable-coefficients-linear and nonlinear partial differential equations...
- Fourier transformFourier transformIn mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
- Pseudodifferential operator
- Oscillatory integral operator