
Fractional Schrödinger equation
Encyclopedia
The fractional Schrödinger equation is a fundamental equation of fractional quantum mechanics
. It was discovered by Nick Laskin (1999) as a result of extending the Feynman path integral, from the Brownian-like to Lévy-like quantum mechanical paths. The term fractional Schrödinger equation was coined by Nick Laskin. The fractional Schrödinger equation has the following form :
Fractional quantum mechanics
In physics, fractional quantum mechanics is a generalization of standard quantum mechanics. The term fractional quantum mechanics was coined by Nick Laskin...
. It was discovered by Nick Laskin (1999) as a result of extending the Feynman path integral, from the Brownian-like to Lévy-like quantum mechanical paths. The term fractional Schrödinger equation was coined by Nick Laskin. The fractional Schrödinger equation has the following form :
-

Here is a 3-dimensional vector,
is a 3-dimensional vector,  is the Planck constantPlanck constantThe Planck constant , also called Planck's constant, is a physical constant reflecting the sizes of energy quanta in quantum mechanics. It is named after Max Planck, one of the founders of quantum theory, who discovered it in 1899...
is the Planck constantPlanck constantThe Planck constant , also called Planck's constant, is a physical constant reflecting the sizes of energy quanta in quantum mechanics. It is named after Max Planck, one of the founders of quantum theory, who discovered it in 1899...
,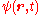 is the wavefunctionWavefunctionNot to be confused with the related concept of the Wave equationA wave function or wavefunction is a probability amplitude in quantum mechanics describing the quantum state of a particle and how it behaves. Typically, its values are complex numbers and, for a single particle, it is a function of...
is the wavefunctionWavefunctionNot to be confused with the related concept of the Wave equationA wave function or wavefunction is a probability amplitude in quantum mechanics describing the quantum state of a particle and how it behaves. Typically, its values are complex numbers and, for a single particle, it is a function of...
, which is the quantum mechanical probability amplitude for the particle to have a given position at any given time t,
at any given time t, 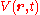 is a potential energy, and
is a potential energy, and 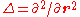 is the Laplace operatorLaplace operatorIn mathematics the Laplace operator or Laplacian is a differential operator given by the divergence of the gradient of a function on Euclidean space. It is usually denoted by the symbols ∇·∇, ∇2 or Δ...
is the Laplace operatorLaplace operatorIn mathematics the Laplace operator or Laplacian is a differential operator given by the divergence of the gradient of a function on Euclidean space. It is usually denoted by the symbols ∇·∇, ∇2 or Δ...
. Further,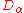 is a scale constant with physical dimension
is a scale constant with physical dimension  , (at α = 2, D2 =1/2m, where m is a particle mass), and the operator
, (at α = 2, D2 =1/2m, where m is a particle mass), and the operator 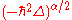 is the 3-dimensional fractional quantum Riesz derivative defined by
is the 3-dimensional fractional quantum Riesz derivative defined by
-
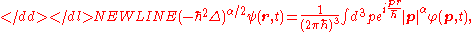
Here the wave functions in the space and momentum
and momentum  representations are related each other by the 3-dimensional Fourier transforms
representations are related each other by the 3-dimensional Fourier transforms
-
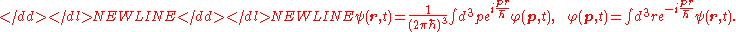
The index α in the fractional Schrödinger equation is the Lévy index, 1 < α ≤ 2. Thus, the fractional Schrödinger equation includes a space derivativeDerivativeIn calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
of fractional order α instead of the second order (α = 2) space derivative in the standard Schrödinger equationSchrödinger equationThe Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....
. Thus, the fractional Schrödinger equation is a fractional differential equation in accordance with modern terminology. This is the main point of the term fractional Schrödinger equation or a more general term fractional quantum mechanicsFractional quantum mechanicsIn physics, fractional quantum mechanics is a generalization of standard quantum mechanics. The term fractional quantum mechanics was coined by Nick Laskin...
. At α = 2 fractional Schrödinger equation becomes the well-known Schrödinger equationSchrödinger equationThe Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....
.
The fractional Schrödinger equation has the following operator form-

where the fractional Hamilton operator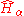 is given by
is given by
-
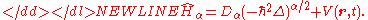
The Hamilton operator,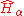 corresponds to classical mechanics Hamiltonian function
corresponds to classical mechanics Hamiltonian function
-

where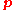 and
and  are the momentum and the coordinate respectively.
are the momentum and the coordinate respectively.
Time-independent fractional Schrödinger equation
The special case when the Hamiltonian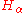 is independent of time
is independent of time
-

is of great importance for physical applications.
It is easy to see that in this case there exist the special solution of the fractional Schrödinger equation-
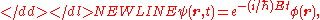
where satisfies
satisfies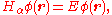
or

This is the time-independent fractional Schrödinger equation.
Thus, we see that the wave function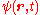 oscillates with a definite frequency. In classical physicsClassical physicsWhat "classical physics" refers to depends on the context. When discussing special relativity, it refers to the Newtonian physics which preceded relativity, i.e. the branches of physics based on principles developed before the rise of relativity and quantum mechanics...
oscillates with a definite frequency. In classical physicsClassical physicsWhat "classical physics" refers to depends on the context. When discussing special relativity, it refers to the Newtonian physics which preceded relativity, i.e. the branches of physics based on principles developed before the rise of relativity and quantum mechanics...
the frequency corresponds to the energy. Therefore, the quantum mechanical state has a definite energy E.
The probability to find a particle at is the absolute square of the wave function
is the absolute square of the wave function 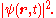
Because of time-independent fractional Schrödinger equation this is equal to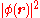 and does not depend upon the time.
and does not depend upon the time.
That is, the probability of finding the particle at is independent of the time. One can say that the system is in a stationary
is independent of the time. One can say that the system is in a stationary
state. In other words, there is no variation in the probabilities as a function of time.
See also
- Fractional quantum mechanicsFractional quantum mechanicsIn physics, fractional quantum mechanics is a generalization of standard quantum mechanics. The term fractional quantum mechanics was coined by Nick Laskin...
- Schrödinger equationSchrödinger equationThe Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....
- Path integral formulationPath integral formulationThe path integral formulation of quantum mechanics is a description of quantum theory which generalizes the action principle of classical mechanics...
- Relation between Schrödinger's equation and the path integral formulation of quantum mechanicsRelation between Schrödinger's equation and the path integral formulation of quantum mechanicsThis article relates the Schrödinger equation with the path integral formulation of quantum mechanics using a simple nonrelativistic one-dimensional single-particle Hamiltonian composed of kinetic and potential energy.-Schrödinger's equation:...
- Fractional calculusFractional calculusFractional calculus is a branch of mathematical analysis that studies the possibility of taking real number powers or complex number powers of the differentiation operator.and the integration operator J...
- Fractional quantum mechanics
-
-
-
-
-
-
-

