
Fractional coordinates
Encyclopedia
In crystallography
, a fractional coordinate system is a coordinate system in which the edges of the unit cell are used as the basic vectors to describe the positions of atomic nuclei. The unit cell is a parallelepiped
defined by the lengths of its edges a, b, c and angles between them α, β, γ as shown in the figure below.

, the a-axis is collinear with the x-axis, and the b-axis lies in the xy-plane, fractional coordinates can be converted to cartesian coordinates through the following transformation matrix:
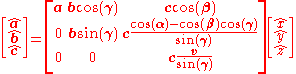
where

For the special case of a monoclinic cell
(a common case) where α=γ=90° and β>90°, this gives:
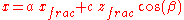


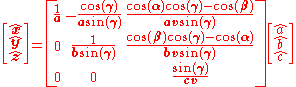
Crystallography
Crystallography is the experimental science of the arrangement of atoms in solids. The word "crystallography" derives from the Greek words crystallon = cold drop / frozen drop, with its meaning extending to all solids with some degree of transparency, and grapho = write.Before the development of...
, a fractional coordinate system is a coordinate system in which the edges of the unit cell are used as the basic vectors to describe the positions of atomic nuclei. The unit cell is a parallelepiped
Parallelepiped
In geometry, a parallelepiped is a three-dimensional figure formed by six parallelograms. By analogy, it relates to a parallelogram just as a cube relates to a square. In Euclidean geometry, its definition encompasses all four concepts...
defined by the lengths of its edges a, b, c and angles between them α, β, γ as shown in the figure below.

Conversion to cartesian coordinates
If the fractional coordinate system has the same origin as the cartesian coordinate systemCartesian coordinate system
A Cartesian coordinate system specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length...
, the a-axis is collinear with the x-axis, and the b-axis lies in the xy-plane, fractional coordinates can be converted to cartesian coordinates through the following transformation matrix:
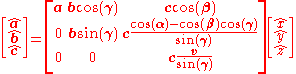
where

For the special case of a monoclinic cell
Monoclinic crystal system
In crystallography, the monoclinic crystal system is one of the 7 lattice point groups. A crystal system is described by three vectors. In the monoclinic system, the crystal is described by vectors of unequal length, as in the orthorhombic system. They form a rectangular prism with a...
(a common case) where α=γ=90° and β>90°, this gives:
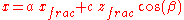


Conversion from cartesian coordinates
The above fractional-to-cartesian transformation can be inverted as follows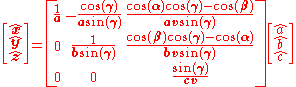
External links
- Practical transformation matrices in crystallography- includes an online coordinate converter

