Free field
Encyclopedia
In classical physics
, a free field is a field
whose equations of motion are given by linear
partial differential equation
s. Such linear PDE's have a unique solution for a given initial condition.
In quantum field theory
, an operator valued distribution is a free field if it satisfies some linear
partial differential equation
s such that the corresponding case of the same linear PDEs for a classical field (i.e. not an operator) would be the Euler-Lagrange equation
for some quadratic
Lagrangian
. We can differentiate distributions by defining their derivatives via differentiated test functions. See Schwartz distribution for more details. Since we are dealing not with ordinary distributions but operator valued distributions, it is understood these PDEs aren't constraints on states but instead a description of the relations among the smeared fields. Beside the PDEs, the operators also satisfy another relation, the commutation/anticommutation relations.
Basically, commutator
(for boson
s)/anticommutator (for fermions) of two smeared fields is i times the Peierls bracket
of the field with itself (which is really a distribution, not a function) for the PDEs smeared over both test functions. This has the form of a CCR/CAR algebra.
CCR/CAR algebras with infinitely many degrees of freedom have many inequivalent irreducible unitary representations. If the theory is defined over Minkowski space
, we may choose the unitary irrep containing a vacuum state
although that isn't always necessary.
.
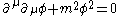This is a bosonic field. Let's call the distribution given by the Peierls bracket Δ.
Then,
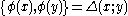
where here, φ is a classical field and {,} is the Peierls bracket.
Then, the canonical commutation relation
relation is
.
Note that Δ is a distribution over two arguments, and so, can be smeared as well.
Equivalently, we could have insisted that
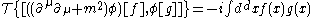
where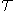
is the time ordering operator and that if the supports of f and g are spacelike separated,
.
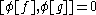Classical physics
What "classical physics" refers to depends on the context. When discussing special relativity, it refers to the Newtonian physics which preceded relativity, i.e. the branches of physics based on principles developed before the rise of relativity and quantum mechanics...
, a free field is a field
Field
-Places:* Field, British Columbia, Canada* Field, Minneapolis, Minnesota, United States* Field, Ontario, Canada* Field Island, Nunavut, Canada* Mount Field - Expanses of open ground :* Field...
whose equations of motion are given by linear
Linear
In mathematics, a linear map or function f is a function which satisfies the following two properties:* Additivity : f = f + f...
partial differential equation
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
s. Such linear PDE's have a unique solution for a given initial condition.
In quantum field theory
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
, an operator valued distribution is a free field if it satisfies some linear
Linear
In mathematics, a linear map or function f is a function which satisfies the following two properties:* Additivity : f = f + f...
partial differential equation
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
s such that the corresponding case of the same linear PDEs for a classical field (i.e. not an operator) would be the Euler-Lagrange equation
Euler-Lagrange equation
In calculus of variations, the Euler–Lagrange equation, Euler's equation, or Lagrange's equation, is a differential equation whose solutions are the functions for which a given functional is stationary...
for some quadratic
Quadratic
In mathematics, the term quadratic describes something that pertains to squares, to the operation of squaring, to terms of the second degree, or equations or formulas that involve such terms...
Lagrangian
Lagrangian
The Lagrangian, L, of a dynamical system is a function that summarizes the dynamics of the system. It is named after Joseph Louis Lagrange. The concept of a Lagrangian was originally introduced in a reformulation of classical mechanics by Irish mathematician William Rowan Hamilton known as...
. We can differentiate distributions by defining their derivatives via differentiated test functions. See Schwartz distribution for more details. Since we are dealing not with ordinary distributions but operator valued distributions, it is understood these PDEs aren't constraints on states but instead a description of the relations among the smeared fields. Beside the PDEs, the operators also satisfy another relation, the commutation/anticommutation relations.
Basically, commutator
Commutator
In mathematics, the commutator gives an indication of the extent to which a certain binary operation fails to be commutative. There are different definitions used in group theory and ring theory.-Group theory:...
(for boson
Boson
In particle physics, bosons are subatomic particles that obey Bose–Einstein statistics. Several bosons can occupy the same quantum state. The word boson derives from the name of Satyendra Nath Bose....
s)/anticommutator (for fermions) of two smeared fields is i times the Peierls bracket
Peierls bracket
In theoretical physics, the Peierls bracket is an equivalent description of the Poisson bracket. It directly follows from the action and does not require the canonical coordinates and their canonical momenta to be defined in advance.The bracket[A,B]...
of the field with itself (which is really a distribution, not a function) for the PDEs smeared over both test functions. This has the form of a CCR/CAR algebra.
CCR/CAR algebras with infinitely many degrees of freedom have many inequivalent irreducible unitary representations. If the theory is defined over Minkowski space
Minkowski space
In physics and mathematics, Minkowski space or Minkowski spacetime is the mathematical setting in which Einstein's theory of special relativity is most conveniently formulated...
, we may choose the unitary irrep containing a vacuum state
Vacuum state
In quantum field theory, the vacuum state is the quantum state with the lowest possible energy. Generally, it contains no physical particles...
although that isn't always necessary.
Example
Let φ be an operator valued distribution and the (Klein-Gordon) PDE be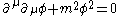.This is a bosonic field. Let's call the distribution given by the Peierls bracket Δ.
Then,
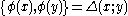
where here, φ is a classical field and {,} is the Peierls bracket.
Then, the canonical commutation relation
Canonical commutation relation
In physics, the canonical commutation relation is the relation between canonical conjugate quantities , for example:[x,p_x] = i\hbar...
relation is
.Note that Δ is a distribution over two arguments, and so, can be smeared as well.
Equivalently, we could have insisted that
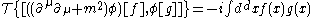
where
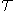is the time ordering operator and that if the supports of f and g are spacelike separated,.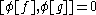