
Friedman translation
Encyclopedia
In mathematical logic
, the Friedman translation is a certain transformation of intuitionistic
formula
s. Among other things it can be used to show that the Π02
-theorems of various first-order theories of classical mathematics are also theorems of intuitionistic mathematics. It is named after its discoverer, Harvey Friedman
.
results. The key condition is that the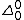 sentences of the logic be decidable, allowing the unquantified theorems of the intuitionistic and classical theories to coincide.
sentences of the logic be decidable, allowing the unquantified theorems of the intuitionistic and classical theories to coincide.
For example, if A is provable in Heyting arithmetic
(HA), then AB is also provable in HA. Moreover, if A is a Σ01-formula
, then AB is in HA equivalent to . This implies that:
Mathematical logic
Mathematical logic is a subfield of mathematics with close connections to foundations of mathematics, theoretical computer science and philosophical logic. The field includes both the mathematical study of logic and the applications of formal logic to other areas of mathematics...
, the Friedman translation is a certain transformation of intuitionistic
Intuitionistic logic
Intuitionistic logic, or constructive logic, is a symbolic logic system differing from classical logic in its definition of the meaning of a statement being true. In classical logic, all well-formed statements are assumed to be either true or false, even if we do not have a proof of either...
formula
Well-formed formula
In mathematical logic, a well-formed formula, shortly wff, often simply formula, is a word which is part of a formal language...
s. Among other things it can be used to show that the Π02
Arithmetical hierarchy
In mathematical logic, the arithmetical hierarchy, arithmetic hierarchy or Kleene-Mostowski hierarchy classifies certain sets based on the complexity of formulas that define them...
-theorems of various first-order theories of classical mathematics are also theorems of intuitionistic mathematics. It is named after its discoverer, Harvey Friedman
Harvey Friedman
Harvey Friedman is a mathematical logician at Ohio State University in Columbus, Ohio. He is noted especially for his work on reverse mathematics, a project intended to derive the axioms of mathematics from the theorems considered to be necessary...
.
Definition
Let A and B be intuitionistic formulas, where no free variable of B is quantified in A. The translation AB is defined by replacing each atomic subformula C of A by . For purposes of the translation, ⊥ is considered to be an atomic formula as well, hence it is replaced with (which is equivalent to B). Note that ¬A is defined as an abbreviation for henceApplication
The Friedman translation can be used to show the closure of many intuitionistic theories under the Markov rule, and to obtain partial conservativityConservative extension
In mathematical logic, a logical theory T_2 is a conservative extension of a theory T_1 if the language of T_2 extends the language of T_1; every theorem of T_1 is a theorem of T_2; and any theorem of T_2 which is in the language of T_1 is already a theorem of T_1.More generally, if Γ is a set of...
results. The key condition is that the
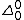 sentences of the logic be decidable, allowing the unquantified theorems of the intuitionistic and classical theories to coincide.
sentences of the logic be decidable, allowing the unquantified theorems of the intuitionistic and classical theories to coincide.For example, if A is provable in Heyting arithmetic
Heyting arithmetic
In mathematical logic, Heyting arithmetic is an axiomatization of arithmetic in accordance with the philosophy of intuitionism. It is named after Arend Heyting, who first proposed it....
(HA), then AB is also provable in HA. Moreover, if A is a Σ01-formula
Arithmetical hierarchy
In mathematical logic, the arithmetical hierarchy, arithmetic hierarchy or Kleene-Mostowski hierarchy classifies certain sets based on the complexity of formulas that define them...
, then AB is in HA equivalent to . This implies that:
- Heyting arithmetic is closed under the primitive recursive Markov rule (MPPR): if the formula ¬¬A is provable in HA, where A is a Σ01-formula, then A is also provable in HA.
- Peano arithmetic is Π02-conservative over Heyting arithmetic: if Peano arithmetic proves a Π02-formula A, then A is already provable in HA.

