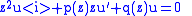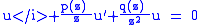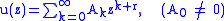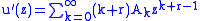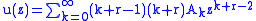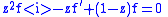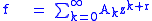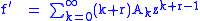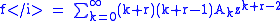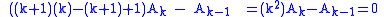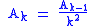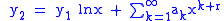Frobenius method
Encyclopedia
In mathematics
, the Frobenius method, named after Ferdinand Georg Frobenius
, is a way to find an infinite series solution for a second-order ordinary differential equation
of the form
in the vicinity of the regular singular point z=0.
We can divide by z2 to obtain a differential equation of the form
which will not be solvable with regular power series methods if either p(z)/z or q(z)/z2 are not analytic
at z = 0. The Frobenius method enables us to create a power series solution to such a differential equation, provided that p(z) and q(z) are themselves analytic at 0 or, being analytic elsewhere, both their limits at 0 exist (and are finite).
Differentiating:
Substituting: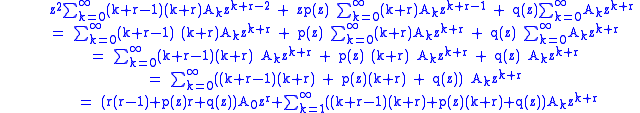
The expression
is known as the indicial polynomial, which is quadratic in r. The general definition of the indicial polynomial is the coefficient of the lowest power of z in the infinite series. In this case it happens to be that this is the rth coefficient but, it is possible for the lowest possible exponent to be r − 2, r − 1 or, something else depending on the given differential equation. This detail is important to keep in mind because one can end up with complicated expressions in the process of synchronizing all the series of the differential equation to start at the same index value which in the above expression is k = 1. However, in solving for the indicial roots attention is focused only on the coefficient of the lowest power of z.
Using this, the general expression of the coefficient of zk + r is
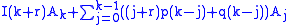
These coefficients must be zero, since they should be solutions of the differential equation, so
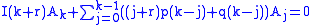
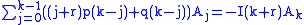
The series solution with Ak above,
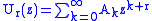
satisfies
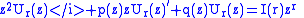
If we choose one of the roots to the indicial polynomial for r in Ur(z), we gain a solution to the differential equation. If the difference between the roots is not an integer, we get another, linearly independent solution in the other root.
Divide throughout by z2 to give
which has the requisite singularity at z = 0.
Use the series solution
Now, substituting
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Frobenius method, named after Ferdinand Georg Frobenius
Ferdinand Georg Frobenius
Ferdinand Georg Frobenius was a German mathematician, best known for his contributions to the theory of differential equations and to group theory...
, is a way to find an infinite series solution for a second-order ordinary differential equation
Ordinary differential equation
In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
of the form
in the vicinity of the regular singular point z=0.
We can divide by z2 to obtain a differential equation of the form
which will not be solvable with regular power series methods if either p(z)/z or q(z)/z2 are not analytic
Analytic function
In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...
at z = 0. The Frobenius method enables us to create a power series solution to such a differential equation, provided that p(z) and q(z) are themselves analytic at 0 or, being analytic elsewhere, both their limits at 0 exist (and are finite).
Explanation
The Frobenius method tells us that we can seek a power series solution of the form
Differentiating:
Substituting:
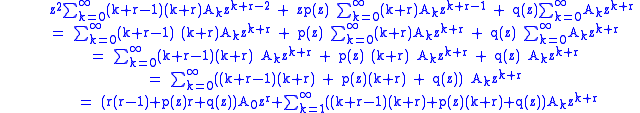
The expression
is known as the indicial polynomial, which is quadratic in r. The general definition of the indicial polynomial is the coefficient of the lowest power of z in the infinite series. In this case it happens to be that this is the rth coefficient but, it is possible for the lowest possible exponent to be r − 2, r − 1 or, something else depending on the given differential equation. This detail is important to keep in mind because one can end up with complicated expressions in the process of synchronizing all the series of the differential equation to start at the same index value which in the above expression is k = 1. However, in solving for the indicial roots attention is focused only on the coefficient of the lowest power of z.
Using this, the general expression of the coefficient of zk + r is
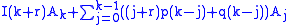
These coefficients must be zero, since they should be solutions of the differential equation, so
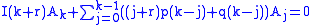
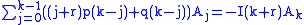
The series solution with Ak above,
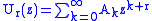
satisfies
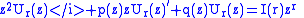
If we choose one of the roots to the indicial polynomial for r in Ur(z), we gain a solution to the differential equation. If the difference between the roots is not an integer, we get another, linearly independent solution in the other root.
Example
Let us solve
Divide throughout by z2 to give
which has the requisite singularity at z = 0.
Use the series solution
Now, substituting
-
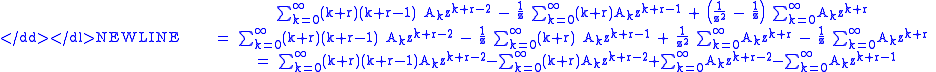
We need to shift the final sum.
-
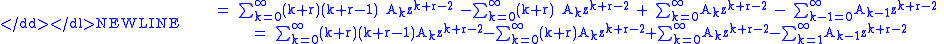
We can take one element out of the sums that start with k=0 to obtain the sums starting at the same index.
-
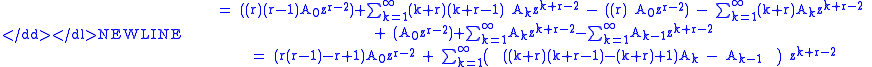
We obtain one linearly independent solution by solving the indicial polynomial r(r − 1) − r + 1 = r2 − 2r + 1 = 0 which gives a double root of 1. Using this root, we set the coefficient of zk + r − 2 to be zero (for it to be a solution), which gives us the recurrence
Given some initial conditions, we can either solve the recurrence entirely or obtain a solution in power series form.
Since the ratio of coefficients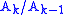
is a rational functionRational functionIn mathematics, a rational function is any function which can be written as the ratio of two polynomial functions. Neither the coefficients of the polynomials nor the values taken by the function are necessarily rational.-Definitions:...
, the power series can be written as a generalized hypergeometric series.
Double roots
The previous example involved an indicial polynomial with a repeated root, which only gave one solution to the given differential equation. In general, the Frobenius method gives two independent solutions provided that the indicial equation's roots are unique.
If the root is repeated, or the roots differ by an integer, then the second solution can be found by the equation:
Where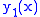
is the first solution and the coefficients 
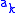are to be determined.
External links
- John H. Mathews, Module for Frobenius Series Solution Chapter 4 contains the full method including proofs.
-
-
-
