
Fréchet surface
Encyclopedia
In mathematics
, a Fréchet surface is an equivalence class of parametrized surfaces in a metric space
. In other words, a Fréchet surface is a way of thinking about surfaces independently of how they are "written down" (parametrized). The concept is named after the French
mathematician
Maurice Fréchet.
2-dimension
al manifold
, either closed
or with boundary
, and let (X, d) be a metric space. A parametrized surface in X is a map

that is continuous with respect to the topology
on M and the metric topology on X. Let

where the infimum
is taken over all homeomorphism
s σ of M to itself. Call two parametrized surfaces f and g in X equivalent if and only if
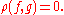
An equivalence class [f] of parametrized surfaces under this notion of equivalence is called a Fréchet surface; each of the parametrized surfaces in this equivalence class is called a parametrization of the Fréchet surface [f].
For example, given two Fréchet surfaces, the value of ρ(f, g) is independent of the choice of the parametrizations f and g, and is called the Fréchet distance between the Fréchet surfaces.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a Fréchet surface is an equivalence class of parametrized surfaces in a metric space
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
. In other words, a Fréchet surface is a way of thinking about surfaces independently of how they are "written down" (parametrized). The concept is named after the French
France
The French Republic , The French Republic , The French Republic , (commonly known as France , is a unitary semi-presidential republic in Western Europe with several overseas territories and islands located on other continents and in the Indian, Pacific, and Atlantic oceans. Metropolitan France...
mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
Maurice Fréchet.
Definitions
Let M be a compactCompact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
2-dimension
Dimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
al manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
, either closed
Closed set
In geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
or with boundary
Boundary (topology)
In topology and mathematics in general, the boundary of a subset S of a topological space X is the set of points which can be approached both from S and from the outside of S. More precisely, it is the set of points in the closure of S, not belonging to the interior of S. An element of the boundary...
, and let (X, d) be a metric space. A parametrized surface in X is a map

that is continuous with respect to the topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
on M and the metric topology on X. Let

where the infimum
Infimum
In mathematics, the infimum of a subset S of some partially ordered set T is the greatest element of T that is less than or equal to all elements of S. Consequently the term greatest lower bound is also commonly used...
is taken over all homeomorphism
Homeomorphism
In the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
s σ of M to itself. Call two parametrized surfaces f and g in X equivalent if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
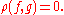
An equivalence class [f] of parametrized surfaces under this notion of equivalence is called a Fréchet surface; each of the parametrized surfaces in this equivalence class is called a parametrization of the Fréchet surface [f].
Properties
Many properties of parametrized surfaces are actually properties of the Fréchet surface, i.e. of the whole equivalence class, and not of any particular parametrization.For example, given two Fréchet surfaces, the value of ρ(f, g) is independent of the choice of the parametrizations f and g, and is called the Fréchet distance between the Fréchet surfaces.

