
Fundamental lemma of sieve theory
Encyclopedia
In number theory
, the fundamental lemma of sieve theory is any of several results that systematize the process of applying sieve methods to particular problems. Halberstam
& Richert
write:
Diamond & Halberstam
attribute the terminology Fundamental Lemma to Jonas Kubilius
.
& Richert
, in Greaves,
and in Friedlander
& Iwaniec
.
We make the assumptions:
There is a parameter u ≥ 1 that is at our disposal. We have uniformly in A, X, z, and u that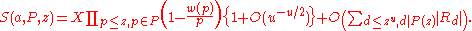
In applications we pick u to get the best error term. In the sieve it represents the number of levels of the inclusion–exclusion principle.
& Richert
. Another formulation is in Diamond & Halberstam
.
We make the assumptions:
The fundamental lemma has almost the same form as for the combinatorial sieve. Write u = ln X / ln z. The conclusion is:
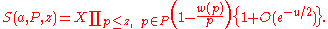
Note that u is no longer an independent parameter at our disposal, but is controlled by the choice of z.
Note that the error term here is weaker than for the fundamental lemma of the combinatorial sieve. Halberstam & Richert remark: "Thus it is not true to say, as has been asserted from time to time in the literature, that Selberg's sieve is always better than Brun's."
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, the fundamental lemma of sieve theory is any of several results that systematize the process of applying sieve methods to particular problems. Halberstam
Heini Halberstam
Heini Halberstam is a British mathematician, working in the field of analytic number theory. He is one of the two mathematicians after whom the Elliott-Halberstam conjecture is named....
& Richert
Hans-Egon Richert
Hans-Egon Richert was a German mathematician who worked primarily in analytic number theory. He is the author of a definitive bookon sieve theory.-Life and education:...
write:
Diamond & Halberstam
Heini Halberstam
Heini Halberstam is a British mathematician, working in the field of analytic number theory. He is one of the two mathematicians after whom the Elliott-Halberstam conjecture is named....
attribute the terminology Fundamental Lemma to Jonas Kubilius
Jonas Kubilius
Jonas Kubilius was a Lithuanian mathematician who worked in probability theory and number theory. He was rector of Vilnius University for 32 years, and served one term in the Lithuanian parliament.-Life and education:...
.
Common notation
We use these notations:- A is a set of X positive integers, and Ad is its subset of integers divisible by d
- w(d) and Rd are functions of A and of d that estimate the number of elements of A that are divisible by d, according to the formula
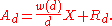
- Thus w(d) / d represents an approximate density of members divisible by d, and Rd represents an error or remainder term.
- P is a set of primes, and P(z) is its the product of those primes ≤ z
- S(A, P, z) is the number of elements of A not divisible by any prime in P that is ≤ z
- κ is a constant, called the sifting density, that appears in the assumptions below. It is a weighted average of the number of residue classes sieved out by each prime.
Fundamental lemma of the combinatorial sieve
This formulation is from Tenenbaum. Other formulations are in HalberstamHeini Halberstam
Heini Halberstam is a British mathematician, working in the field of analytic number theory. He is one of the two mathematicians after whom the Elliott-Halberstam conjecture is named....
& Richert
Hans-Egon Richert
Hans-Egon Richert was a German mathematician who worked primarily in analytic number theory. He is the author of a definitive bookon sieve theory.-Life and education:...
, in Greaves,
and in Friedlander
John Friedlander
John Benjamin Friedlander is a Canadian mathematician specializing in analytic number theory. He received his B.Sc. from the University of Toronto in 1965, an M.A. from the University of Waterloo in 1966, and a Ph.D. from Pennsylvania State University in 1972. He was a lecturer at M.I.T...
& Iwaniec
Henryk Iwaniec
Henryk Iwaniec is a Polish American mathematician, and since 1987 a professor at Rutgers University. He was awarded the fourteenth Frank Nelson Cole Prize in Number Theory in 2002. He received the Leroy P. Steele Prize for Mathematical Exposition in 2011.-Background and education:Iwaniec studied...
.
We make the assumptions:
- w(d) is a multiplicative functionMultiplicative functionIn number theory, a multiplicative function is an arithmetic function f of the positive integer n with the property that f = 1 and whenevera and b are coprime, then...
. - The sifting density κ satisfies, for some constant C and any real numbers η and ξ with 2 ≤ η ≤ ξ:

There is a parameter u ≥ 1 that is at our disposal. We have uniformly in A, X, z, and u that
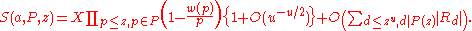
In applications we pick u to get the best error term. In the sieve it represents the number of levels of the inclusion–exclusion principle.
Fundamental lemma of the Selberg sieve
This formulation is from HalberstamHeini Halberstam
Heini Halberstam is a British mathematician, working in the field of analytic number theory. He is one of the two mathematicians after whom the Elliott-Halberstam conjecture is named....
& Richert
Hans-Egon Richert
Hans-Egon Richert was a German mathematician who worked primarily in analytic number theory. He is the author of a definitive bookon sieve theory.-Life and education:...
. Another formulation is in Diamond & Halberstam
Heini Halberstam
Heini Halberstam is a British mathematician, working in the field of analytic number theory. He is one of the two mathematicians after whom the Elliott-Halberstam conjecture is named....
.
We make the assumptions:
- w(d) is a multiplicative functionMultiplicative functionIn number theory, a multiplicative function is an arithmetic function f of the positive integer n with the property that f = 1 and whenevera and b are coprime, then...
. - The sifting density κ satisfies, for some constant C and any real numbers η and ξ with 2 ≤ η ≤ ξ:

- w(p) / p < 1 - c for some small fixed c and all p
- | Rd | ≤ ω(d) where ω(d) is the number of distinct prime divisors of d.
The fundamental lemma has almost the same form as for the combinatorial sieve. Write u = ln X / ln z. The conclusion is:
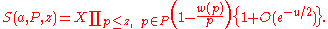
Note that u is no longer an independent parameter at our disposal, but is controlled by the choice of z.
Note that the error term here is weaker than for the fundamental lemma of the combinatorial sieve. Halberstam & Richert remark: "Thus it is not true to say, as has been asserted from time to time in the literature, that Selberg's sieve is always better than Brun's."

