
Fundamental recurrence formulas
Encyclopedia
In the theory of continued fractions
, the fundamental recurrence formulas relate the partial numerators and the partial denominators with the numerators and denominators of the fraction's successive convergents
. Let

be a general continued fraction, where the an (the partial numerators) and the bn (the partial denominators) are numbers. Denoting the successive numerators and denominators of the fraction by An and Bn, respectively, the fundamental recurrence formulas are given by
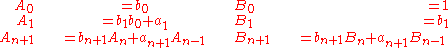
The continued fraction's successive convergents are then given by
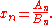
These recurrence relations are due to John Wallis (1616-1703).
, that the determinant formula
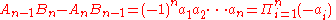
holds for all positive integers n > 0. If neither Bn-1 nor Bn is zero, this relationship can also be used to express the difference between two successive convergents of the continued fraction.
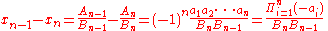
It is necessary but not sufficient for the convergence of an infinite continued fraction that the difference between successive convergents approaches zero; this is the subject of
the convergence problem.
that represents the golden ratio φ
:

Applying the fundamental recurrence formulas we find that the successive numerators An are {1, 2, 3, 5, 8, 13, ...} and the successive denominators Bn are {1, 1, 2, 3, 5, 8, ...}, the Fibonacci number
s. Since all the partial numerators in this example are equal to one, the determinant formula assures us that the absolute value of the difference between successive convergents approaches zero quite rapidly.
Generalized continued fraction
In complex analysis, a branch of mathematics, a generalized continued fraction is a generalization of regular continued fractions in canonical form, in which the partial numerators and partial denominators can assume arbitrary real or complex values....
, the fundamental recurrence formulas relate the partial numerators and the partial denominators with the numerators and denominators of the fraction's successive convergents
Convergent (continued fraction)
A convergent is one of a sequence of values obtained by evaluating successive truncations of a continued fraction The nth convergent is also known as the nth approximant of a continued fraction.-Representation of real numbers:...
. Let

be a general continued fraction, where the an (the partial numerators) and the bn (the partial denominators) are numbers. Denoting the successive numerators and denominators of the fraction by An and Bn, respectively, the fundamental recurrence formulas are given by
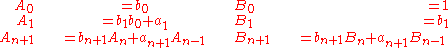
The continued fraction's successive convergents are then given by
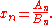
These recurrence relations are due to John Wallis (1616-1703).
The determinant formula
It can be shown, by inductionMathematical induction
Mathematical induction is a method of mathematical proof typically used to establish that a given statement is true of all natural numbers...
, that the determinant formula
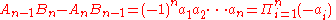
holds for all positive integers n > 0. If neither Bn-1 nor Bn is zero, this relationship can also be used to express the difference between two successive convergents of the continued fraction.
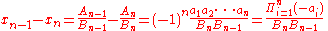
It is necessary but not sufficient for the convergence of an infinite continued fraction that the difference between successive convergents approaches zero; this is the subject of
the convergence problem.
A simple example
Consider the regular continued fraction in canonical formContinued fraction
In mathematics, a continued fraction is an expression obtained through an iterative process of representing a number as the sum of its integer part and the reciprocal of another number, then writing this other number as the sum of its integer part and another reciprocal, and so on...
that represents the golden ratio φ
Golden ratio
In mathematics and the arts, two quantities are in the golden ratio if the ratio of the sum of the quantities to the larger quantity is equal to the ratio of the larger quantity to the smaller one. The golden ratio is an irrational mathematical constant, approximately 1.61803398874989...
:

Applying the fundamental recurrence formulas we find that the successive numerators An are {1, 2, 3, 5, 8, 13, ...} and the successive denominators Bn are {1, 1, 2, 3, 5, 8, ...}, the Fibonacci number
Fibonacci number
In mathematics, the Fibonacci numbers are the numbers in the following integer sequence:0,\;1,\;1,\;2,\;3,\;5,\;8,\;13,\;21,\;34,\;55,\;89,\;144,\; \ldots\; ....
s. Since all the partial numerators in this example are equal to one, the determinant formula assures us that the absolute value of the difference between successive convergents approaches zero quite rapidly.

