
Fundamental theorem of cyclic groups
Encyclopedia
In abstract algebra
, the fundamental theorem of cyclic groups states that every subgroup
of a cyclic group
is cyclic. Moreover, the order
of any subgroup of a cyclic group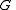 of order
of order 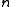 is a divisor of
is a divisor of 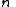 , and for each positive divisor
, and for each positive divisor 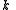 of
of 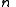 the group
the group 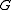 has exactly one subgroup of order
has exactly one subgroup of order 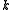 .
.
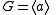 be a cyclic group for some
be a cyclic group for some 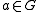 and with identity
and with identity  and order
and order 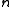 , and let
, and let 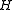 be a subgroup of
be a subgroup of 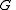 .
.
We will now show that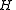 is cyclic. If
is cyclic. If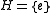 then
then  .
.
If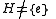 then since
then since  is cyclic every element in
is cyclic every element in  is of the form
is of the form 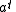 , where
, where  is an integer. Let
is an integer. Let 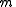 be the least positive integer such that
be the least positive integer such that 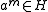 .
.
We will now show that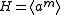 . It follows immediately from the closure property that
. It follows immediately from the closure property that 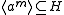 .
.
To show that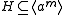 we let
we let 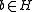 . Since
. Since 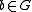 we have that
we have that 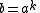 for some positive integer
for some positive integer 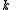 .
.
By the division algorithm
,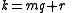 with
with  , and so
, and so
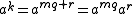 , which yields
, which yields 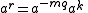 .
.
Now since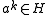 and
and 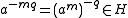 , it follows from closure that
, it follows from closure that 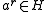 .
.
But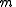 is the least positive integer such that
is the least positive integer such that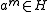 and
and 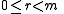 ,
,
which means that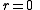 and so
and so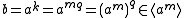 .
.
Thus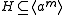 .
.
Since and
and 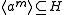 it follows that
it follows that 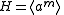 and so
and so 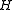 is cyclic.
is cyclic.
We will now show that the order of any subgroup of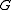 is a divisor of
is a divisor of 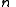 .
.
Let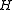 be any subgroup of
be any subgroup of 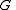 of order
of order 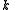 . We have already shown that
. We have already shown that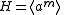 , where
, where 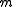
is the least positive integer such that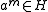 . We know that
. We know that 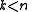 and therefore we can write
and therefore we can write , with
, with 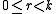 .
.
Since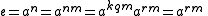 ,
,
we must have :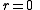 , since
, since 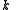 is the smallest positive integer such that
is the smallest positive integer such that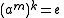 .
.
It follows that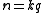 for some integer
for some integer 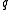 . Thus
. Thus  .
.
We will now prove the last part of the theorem. Let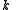 be any positive divisor of
be any positive divisor of 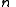 . We will show that
. We will show that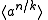
is the one and only subgroup of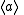 of order
of order  . Note that
. Note that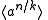
has order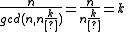 .
.
Let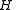 be any subgroup of
be any subgroup of 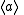 with order
with order 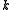 . We know that
. We know that ,
,
where is a divisor of
is a divisor of 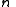 . So
. So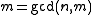 and
and 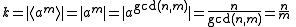 .
.
Consequently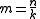 and so
and so 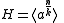 ,
,
and thus the theorem is proved.
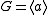 be a cyclic group, and let
be a cyclic group, and let 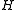 be a subgroup of
be a subgroup of  . Define a morphism
. Define a morphism 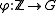 by
by  . Since
. Since 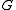 is cyclic generated by
is cyclic generated by  ,
,  is surjective. Let
is surjective. Let  .
. 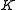 is a subgroup of
is a subgroup of 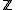 . Since
. Since 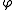 is surjective, the restriction of
is surjective, the restriction of 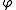 to
to  defines a surjective homomorphism from
defines a surjective homomorphism from 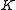 onto
onto 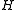 , and therefore
, and therefore 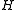 is isomorphic to a quotient of
is isomorphic to a quotient of 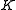 . Since
. Since 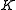 is a subgroup of
is a subgroup of 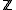 ,
, 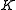 is
is 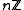 for some integer
for some integer  . If
. If 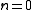 , then
, then 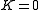 , hence
, hence 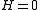 , which is cyclic. Otherwise,
, which is cyclic. Otherwise, 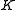 is isomorphic to
is isomorphic to 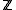 . Therefore
. Therefore 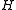 is isomorphic to a quotient of
is isomorphic to a quotient of 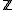 , and they are commonly known to be cyclic.
, and they are commonly known to be cyclic.
which is generated by n elements. Then each submodule of M can also be generated by n elements (and possibly fewer). This result implies the fundamental theorem of cyclic groups by observing that the ring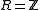 of integers satisfies these conditions, and a cyclic group is precisely a left
of integers satisfies these conditions, and a cyclic group is precisely a left 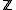 -module which is generated by one element. (Its submodules are its subgroups.)
-module which is generated by one element. (Its submodules are its subgroups.)
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
, the fundamental theorem of cyclic groups states that every subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
of a cyclic group
Cyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
is cyclic. Moreover, the order
Order (group theory)
In group theory, a branch of mathematics, the term order is used in two closely related senses:* The order of a group is its cardinality, i.e., the number of its elements....
of any subgroup of a cyclic group
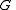 of order
of order 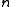 is a divisor of
is a divisor of 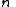 , and for each positive divisor
, and for each positive divisor 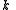 of
of 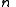 the group
the group 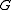 has exactly one subgroup of order
has exactly one subgroup of order 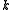 .
.Proof
Let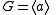 be a cyclic group for some
be a cyclic group for some 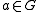 and with identity
and with identity  and order
and order 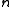 , and let
, and let 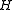 be a subgroup of
be a subgroup of 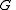 .
.We will now show that
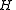 is cyclic. If
is cyclic. If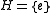 then
then  .
.If
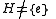 then since
then since  is cyclic every element in
is cyclic every element in  is of the form
is of the form 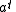 , where
, where  is an integer. Let
is an integer. Let 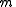 be the least positive integer such that
be the least positive integer such that 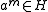 .
.We will now show that
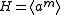 . It follows immediately from the closure property that
. It follows immediately from the closure property that 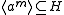 .
.To show that
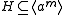 we let
we let 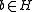 . Since
. Since 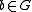 we have that
we have that 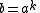 for some positive integer
for some positive integer 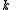 .
.By the division algorithm
Division algorithm
In mathematics, and more particularly in arithmetic, the usual process of division of integers producing a quotient and a remainder can be specified precisely by a theorem stating that these exist uniquely with given properties. An integer division algorithm is any effective method for producing...
,
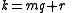 with
with  , and so
, and so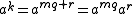 , which yields
, which yields 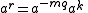 .
.Now since
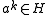 and
and 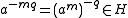 , it follows from closure that
, it follows from closure that 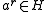 .
.But
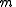 is the least positive integer such that
is the least positive integer such that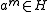 and
and 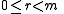 ,
,which means that
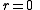 and so
and so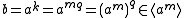 .
.Thus
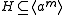 .
.Since
 and
and 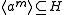 it follows that
it follows that 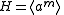 and so
and so 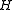 is cyclic.
is cyclic.We will now show that the order of any subgroup of
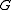 is a divisor of
is a divisor of 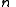 .
.Let
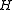 be any subgroup of
be any subgroup of 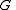 of order
of order 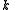 . We have already shown that
. We have already shown that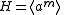 , where
, where 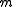
is the least positive integer such that
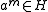 . We know that
. We know that 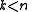 and therefore we can write
and therefore we can write , with
, with 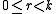 .
.Since
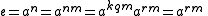 ,
,we must have :
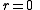 , since
, since 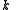 is the smallest positive integer such that
is the smallest positive integer such that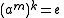 .
.It follows that
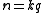 for some integer
for some integer 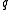 . Thus
. Thus  .
.We will now prove the last part of the theorem. Let
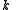 be any positive divisor of
be any positive divisor of 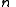 . We will show that
. We will show that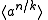
is the one and only subgroup of
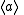 of order
of order  . Note that
. Note that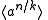
has order
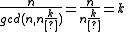 .
.Let
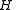 be any subgroup of
be any subgroup of 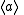 with order
with order 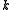 . We know that
. We know that ,
,where
 is a divisor of
is a divisor of 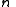 . So
. So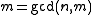 and
and 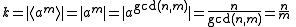 .
.Consequently
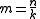 and so
and so 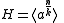 ,
,and thus the theorem is proved.
Proof by homomorphism with integers
Let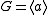 be a cyclic group, and let
be a cyclic group, and let 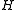 be a subgroup of
be a subgroup of  . Define a morphism
. Define a morphism 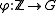 by
by  . Since
. Since 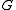 is cyclic generated by
is cyclic generated by  ,
,  is surjective. Let
is surjective. Let  .
. 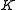 is a subgroup of
is a subgroup of 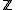 . Since
. Since 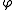 is surjective, the restriction of
is surjective, the restriction of 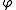 to
to  defines a surjective homomorphism from
defines a surjective homomorphism from 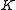 onto
onto 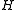 , and therefore
, and therefore 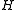 is isomorphic to a quotient of
is isomorphic to a quotient of 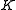 . Since
. Since 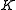 is a subgroup of
is a subgroup of 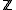 ,
, 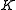 is
is 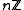 for some integer
for some integer  . If
. If 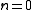 , then
, then 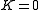 , hence
, hence 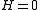 , which is cyclic. Otherwise,
, which is cyclic. Otherwise, 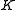 is isomorphic to
is isomorphic to 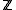 . Therefore
. Therefore 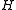 is isomorphic to a quotient of
is isomorphic to a quotient of 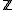 , and they are commonly known to be cyclic.
, and they are commonly known to be cyclic.Converse
The following statements are equivalent.- A group G of order
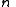 is cyclic.
is cyclic. - For every divisor
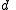 of
of 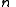 a group G has exactly one subgroup of order
a group G has exactly one subgroup of order 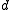 .
. - For every divisor
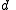 of
of 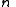 a group G has at most one subgroup of order
a group G has at most one subgroup of order 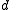 .
.
Generalization
Suppose that R is a right Ore domain in which every left ideal is principal, and let M be a left R-moduleModule (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
which is generated by n elements. Then each submodule of M can also be generated by n elements (and possibly fewer). This result implies the fundamental theorem of cyclic groups by observing that the ring
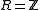 of integers satisfies these conditions, and a cyclic group is precisely a left
of integers satisfies these conditions, and a cyclic group is precisely a left 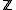 -module which is generated by one element. (Its submodules are its subgroups.)
-module which is generated by one element. (Its submodules are its subgroups.)

