Fuzzy sphere
Encyclopedia
In mathematics
, the fuzzy sphere is one of the simplest and most canonical examples of non-commutative geometry. Ordinarily, the functions defined on a sphere
form a commuting algebra. A fuzzy sphere differs from an ordinary sphere because the algebra of functions on it is not commutative. It is generated by spherical harmonic
s whose spin l is at most equal to some j. The terms in the product of two spherical harmonics that involve spherical harmonics with spin exceeding j are simply omitted in the product. This truncation replaces an infinite-dimensional commutative algebra by a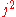
-dimensional non-commutative algebra.
The simplest way to see this sphere is to realize this truncated algebra of functions as a matrix algebra on some finite dimensional vector space.
Take the three j-dimensional matrices
that form a basis for the j dimensional irreducible representation of the Lie algebra SU(2)
. They satisfy the relations
, where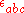 
is the totally antisymmetric symbol
with
, and generate via the matrix product the algebra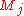 
of j dimensional matrices. The value of the SU(2) Casimir operator in this representation is
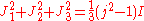
where I is the j-dimensional identity matrix.
Thus, if we define the 'coordinates'
where r is the radius of the sphere and k is a parameter, related to r and j by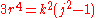
, then the above equation concerning the Casimir operator can be rewritten as
,
which is the usual relation for the coordinates on a sphere of radius r embedded in three dimensional space.
One can define an integral on this space, by
where F is the matrix corresponding to the function f.
For example, the integral of unity, which gives the surface of the sphere in the commutative case is here equal to
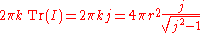
which converges to the value of the surface of the sphere if one takes j to infinity.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the fuzzy sphere is one of the simplest and most canonical examples of non-commutative geometry. Ordinarily, the functions defined on a sphere
Sphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
form a commuting algebra. A fuzzy sphere differs from an ordinary sphere because the algebra of functions on it is not commutative. It is generated by spherical harmonic
Spherical Harmonic
Spherical Harmonic is a science fiction novel from the Saga of the Skolian Empire by Catherine Asaro. It tells the story of Dyhianna Selei , the Ruby Pharaoh of the Skolian Imperialate, as she strives to reform her government and reunite her family in the aftermath of a devastating interstellar...
s whose spin l is at most equal to some j. The terms in the product of two spherical harmonics that involve spherical harmonics with spin exceeding j are simply omitted in the product. This truncation replaces an infinite-dimensional commutative algebra by a
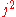-dimensional non-commutative algebra.The simplest way to see this sphere is to realize this truncated algebra of functions as a matrix algebra on some finite dimensional vector space.
Take the three j-dimensional matrices
that form a basis for the j dimensional irreducible representation of the Lie algebra SU(2)Special unitary group
The special unitary group of degree n, denoted SU, is the group of n×n unitary matrices with determinant 1. The group operation is that of matrix multiplication...
. They satisfy the relations
, where 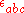is the totally antisymmetric symbolLevi-Civita symbol
The Levi-Civita symbol, also called the permutation symbol, antisymmetric symbol, or alternating symbol, is a mathematical symbol used in particular in tensor calculus...
with
, and generate via the matrix product the algebra 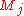of j dimensional matrices. The value of the SU(2) Casimir operator in this representation is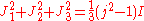where I is the j-dimensional identity matrix.
Thus, if we define the 'coordinates'
where r is the radius of the sphere and k is a parameter, related to r and j by
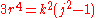, then the above equation concerning the Casimir operator can be rewritten as,which is the usual relation for the coordinates on a sphere of radius r embedded in three dimensional space.
One can define an integral on this space, by
where F is the matrix corresponding to the function f.
For example, the integral of unity, which gives the surface of the sphere in the commutative case is here equal to
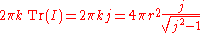
which converges to the value of the surface of the sphere if one takes j to infinity.