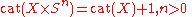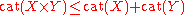Ganea conjecture
Encyclopedia
Ganea's conjecture is a claim in algebraic topology
, now disproved. It states that
where cat(X) is the Lusternik–Schnirelmann category of a topological space
X, and Sn is the n dimensional sphere
.
The inequality
holds for any pair of spaces, X and Y. Furthermore, cat(Sn)=1, for any sphere Sn, n>0. Thus, the conjecture amounts to cat(X × Sn) ≥ cat(X) + 1.
The conjecture was formulated by Tudor Ganea
in 1971. Many particular cases of this conjecture were proved, till finally Norio Iwase gave a counterexample in 1998. In a follow-up paper from 2002, Iwase gave an even stronger counterexample, with X a closed, smooth manifold. This counterexample also disproved a related conjecture, stating that
for a closed manifold M and p a point in M.
This work raises the question: For which spaces X is the Ganea condition, cat(X × Sn) = cat(X) + 1, satisfied? It has been conjectured that these are precisely the spaces X for which cat(X) equals a related invariant, Qcat(X).
Algebraic topology
Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
, now disproved. It states that
where cat(X) is the Lusternik–Schnirelmann category of a topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
X, and Sn is the n dimensional sphere
Sphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
.
The inequality
holds for any pair of spaces, X and Y. Furthermore, cat(Sn)=1, for any sphere Sn, n>0. Thus, the conjecture amounts to cat(X × Sn) ≥ cat(X) + 1.
The conjecture was formulated by Tudor Ganea
Tudor Ganea
Tudor Ganea was a Romanian mathematician, known for his work in algebraic topology, especially homotopy theory. Ganea left Communist Romania to settle in the United States in the early 1960s...
in 1971. Many particular cases of this conjecture were proved, till finally Norio Iwase gave a counterexample in 1998. In a follow-up paper from 2002, Iwase gave an even stronger counterexample, with X a closed, smooth manifold. This counterexample also disproved a related conjecture, stating that
for a closed manifold M and p a point in M.
This work raises the question: For which spaces X is the Ganea condition, cat(X × Sn) = cat(X) + 1, satisfied? It has been conjectured that these are precisely the spaces X for which cat(X) equals a related invariant, Qcat(X).