A Gaussian surface is a closed surface

Surface

In mathematics, specifically in topology, a surface is a two-dimensional topological manifold. The most familiar examples are those that arise as the boundaries of solid objects in ordinary three-dimensional Euclidean space R3 — for example, the surface of a ball...

 in three dimensional space through which the flux

Flux

In the various subfields of physics, there exist two common usages of the term flux, both with rigorous mathematical frameworks.* In the study of transport phenomena , flux is defined as flow per unit area, where flow is the movement of some quantity per time...

 of an electromagnetic field

Electromagnetic field

An electromagnetic field is a physical field produced by moving electrically charged objects. It affects the behavior of charged objects in the vicinity of the field. The electromagnetic field extends indefinitely throughout space and describes the electromagnetic interaction...

 is calculated. It is an arbitrary closed surface used in conjunction with Gauss's law

Gauss's law

In physics, Gauss's law, also known as Gauss's flux theorem, is a law relating the distribution of electric charge to the resulting electric field. Gauss's law states that:...

 in order to calculate the total enclosed electric charge

Electric charge

Electric charge is a physical property of matter that causes it to experience a force when near other electrically charged matter. Electric charge comes in two types, called positive and negative. Two positively charged substances, or objects, experience a mutual repulsive force, as do two...

 by performing a surface integral

Surface integral

In mathematics, a surface integral is a definite integral taken over a surface ; it can be thought of as the double integral analog of the line integral...

, or alternatively, to calculate the electric field of a particular charge distribution.

Gaussian surfaces are usually carefully chosen to exploit symmetries of a situation to simplify the calculation of the surface integral

Surface integral

In mathematics, a surface integral is a definite integral taken over a surface ; it can be thought of as the double integral analog of the line integral...

. If the Gaussian surface is chosen such that for every point on the surface the component of the electric field along the normal vector is constant, then the calculation will not require difficult integration as the constant can be pulled out of the integration sign.

Common Gaussian surfaces

When performing the closed surface integral, the Gaussian surface (commonly abbreviated G.S. or g.s.) does not necessarily encompass all the charge; i.e., there can be arbitrary charges outside the volume: as mentioned,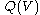 only counts the interior contribution. Furthermore: it is not necessary to choose a Gaussian surface that utilises the symmetry of a situation (as in the examples below) but, obviously the calculations are much less laborious if an appropriate surface is chosen. Most calculations using Gaussian surfaces begin by implementing Gauss' law: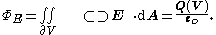


Thereby 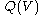is the electrical charge contained in the interior, V, of the closed surface.

This is Gauss's law, combining both the divergence theorem and Coulomb's statement.

Spherical surface

A spherical Gaussian surface is used when finding the electric field or the flux produced by any of the following:

• a point charge
• a uniformly distributed spherical shell of charge
• any other charge distribution with spherical symmetry

The spherical Gaussian surface is chosen so that it is concentric with the charge distribution.

As an example, consider a charged spherical shell of negligible thickness, with a uniformly distributed charge Q and radius R. We can use Gauss's law to find the magnitude of the resultant electric field E at a distance r from the center of the charged shell. It is immediately apparent that for a spherical Gaussian surface of radius r < R the enclosed charge is zero: hence the net flux is zero and the magnitude of the electric field on the Gaussian surface is also 0 (by letting Q_A = 0 in Gauss's law, where Q_A is the charge enclosed by the Gaussian surface).

With the same example, using a larger Gaussian surface outside the shell where r > R, Gauss's law will produce a non-zero electric field. This is determined as follows:

This non-trivial result shows that any spherical distribution of charge acts as a point charge when observed from the outside of the charge distribution; this is in fact a verification of Coulomb's law

Coulomb's law

Coulomb's law or Coulomb's inverse-square law, is a law of physics describing the electrostatic interaction between electrically charged particles. It was first published in 1785 by French physicist Charles Augustin de Coulomb and was essential to the development of the theory of electromagnetism...

. And, as mentioned, any exterior charges don't count.

Cylindrical surface

A cylindrical Gaussian surface is used when finding the electric field or the flux produced by any of the following:

• an infinitely long line of uniform charge
• an infinite plane of uniform charge

As an example "field near infinite line charge" is given below;

Consider a point P at a distance r from an infinite line charge having charge density (charge per unit length) λ (lambda).
Imagine a closed surface in the form of cylinder around line charge in its wall.

If h is the length of cylinder, then charge enclosed in cylinder is
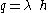
where, q is the charge enclosed in Gaussian surface.
There are three surfaces a, b and c as shown in figure. Now Take differential area "dA" with vector area dA on each surface i.e a, b and c.
Now the flux passing consists of the three contributions

For surfaces a and b, 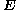and will be perpendicular.
For surface c, and will be parallel, as shown in the figure.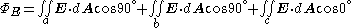


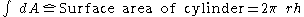
so,

Gauss's law is
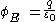
As
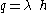
So,
Comparing both makes the following equation'

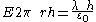
Sample question

Here is a critical thinking question about which the above concepts can be applied.

A slab of insulating material has thickness 2w and is oriented so that its faces are parallel to the yz-plane and given by the planes x=w and x= - w. The y- and z-dimensions of the slab are very large compared to d and may be treated as essentially infinite. The slab has a uniform positive charge density p.

Explain why the electric field due to the slab is zero at the center of the slab (x=0)? The electric field of the slab must be zero by symmetry. There is no preferred direction in the y-z plane, so the electric field can only point in the x-direction. But at the origin in the x-direction, neither the positive nor negative directions should be singled out as special, and so the field must be zero.

Again, only the inner distribution counts, and
again, any cylindrically-symmetric inner charge distribution acts as a line charge centered at the symmetry-axis of the cylinder.

Gaussian pillbox

This surface is most often used to determine the electric field due to an infinite sheet of charge with uniform charge density, or a slab of charge with some finite thickness. The pillbox has a cylindrical shape, and can be thought of as consisting of three components: the disk at one end of the cylinder with area πR², the disk at the other end with equal area, and the side of the cylinder. The sum of the electric flux through each component of the surface is proportional to the enclosed charge of the pillbox, as dictated by Gauss's Law. Because the field close to the sheet can be approximated as constant, the pillbox is oriented in a way so that the field lines penetrate the disks at the ends of the field at a perpendicular angle and the side of the cylinder are parallel to the field lines.

External links

• Fields - a chapter from an online textbook