Gebhart factor
Encyclopedia
The Gebhart factors are used in radiative heat transfer, it is a means to describe the ratio of radiation absorbed by any other surface versus the total emitted radiation from given surface. As such, it becomes the radiation exchange factor between a number of surfaces. The Gebhart factors calculation method is supported in several radiation heat transfer tools, such as TMG and TRASYS.
The method was introduced by Benjamin Gebhart in 1957 . Although a requirement is the calculation of the view factors beforehand, it requires less computational power, compared to using ray tracing with the Monte Carlo Method
(MCM) . Alternative methods are to look at the radiosity
, which Hottel and others build upon.
.
The Gebhart factor approach assumes that the surfaces are gray and emits and are illuminated diffusely and uniformly..
This can be rewritten as:
where
The denominator can also be recognized from the Stefan–Boltzmann law.
The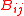
factor can then be used to calculate the net energy transferred from one surface to all other, for an opaque surface given as .:
where
Looking at the geometric relation, it can be seen that:
This can be used to write the net energy transfer from one surface to another, here for 1 to 2:
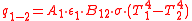
Realizing that this can be used to find the heat transferred (Q), which was used in the definition, and using the view factors as auxiliary equation, it can be shown that the Gebhart factors are :
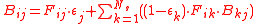
where
And also, from the definition we see that the sum of the Gebhart factors must be equal to 1.
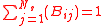
Several approaches exists to describe this as a system of linear equations that can be solved by Gaussian elimination
or similar methods. For simpler cases it can also be formulated as a single expression.
The method was introduced by Benjamin Gebhart in 1957 . Although a requirement is the calculation of the view factors beforehand, it requires less computational power, compared to using ray tracing with the Monte Carlo Method
Monte Carlo method
Monte Carlo methods are a class of computational algorithms that rely on repeated random sampling to compute their results. Monte Carlo methods are often used in computer simulations of physical and mathematical systems...
(MCM) . Alternative methods are to look at the radiosity
Radiosity (heat transfer)
Radiosity is a convenient quantity in optics and heat transfer that represents the total radiation intensity leaving a surface. Radiosity accounts for two components: the radiation being emitted by the surface, and the radiation being reflected from the surface...
, which Hottel and others build upon.
Equations
The Gebhart factor can be given as:.
The Gebhart factor approach assumes that the surfaces are gray and emits and are illuminated diffusely and uniformly..
This can be rewritten as:
where
-
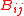is the Gebhart factor
-
is the heat transfer from surface i to j
-
is the emissivityEmissivityThe emissivity of a material is the relative ability of its surface to emit energy by radiation. It is the ratio of energy radiated by a particular material to energy radiated by a black body at the same temperature...
of the surface
-
is the surface area
-
is the temperature
The denominator can also be recognized from the Stefan–Boltzmann law.
The
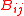factor can then be used to calculate the net energy transferred from one surface to all other, for an opaque surface given as .:where
-
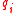is the net heat transfer for surface i
Looking at the geometric relation, it can be seen that:
This can be used to write the net energy transfer from one surface to another, here for 1 to 2:
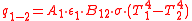
Realizing that this can be used to find the heat transferred (Q), which was used in the definition, and using the view factors as auxiliary equation, it can be shown that the Gebhart factors are :
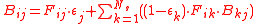
where
-
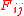is the view factor for surface i to j
And also, from the definition we see that the sum of the Gebhart factors must be equal to 1.
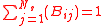
Several approaches exists to describe this as a system of linear equations that can be solved by Gaussian elimination
Gaussian elimination
In linear algebra, Gaussian elimination is an algorithm for solving systems of linear equations. It can also be used to find the rank of a matrix, to calculate the determinant of a matrix, and to calculate the inverse of an invertible square matrix...
or similar methods. For simpler cases it can also be formulated as a single expression.