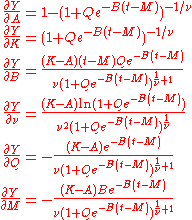The generalised logistic curve or function, also known as Richards' curve is a widely-used and flexible sigmoid function

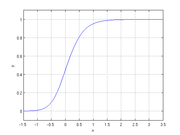
Sigmoid function

Many natural processes, including those of complex system learning curves, exhibit a progression from small beginnings that accelerates and approaches a climax over time. When a detailed description is lacking, a sigmoid function is often used. A sigmoid curve is produced by a mathematical...

 for growth modelling, extending the well-known logistic curve.


where Y = weight, height, size etc., and t = time.

It has six parameters:

• A: the lower asymptote;
• K: the upper asymptote. If A=0 then K is called the carrying capacity;
• B: the growth rate;
• ν>0 : affects near which asymptote maximum growth occurs.
• Q: depends on the value Y(0)
• M: the time of maximum growth if Q=ν

Generalised logistic differential equation

A particular case of Richard's function is:


which is the solution of the so called Richard's differential equation (RDE):


with initial condition


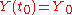
where


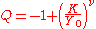
provided that ν > 0 and α > 0.
The classical logistic differential equation is a particular case of the above equation, with ν =1, whereas the Gompertz curve

Gompertz curve

A Gompertz curve or Gompertz function, named after Benjamin Gompertz, is a sigmoid function. It is a type of mathematical model for a time series, where growth is slowest at the start and end of a time period...

 can be recovered in the limit provided that: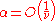


In fact, for small ν it is

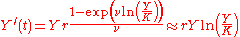
The RDE suits to model many growth phenomena, including the growth of tumours. Concerning its applications in oncology, its main biological features are similar to those of Logistic curve model.

Gradient

When estimating parameters from data, it is often necessary to compute the partial derivatives of the parameters at a given data point t (see ):