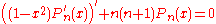Generalized Fourier series
Encyclopedia
In mathematical analysis
, many generalizations of Fourier series
have proved to be useful.
They are all special cases of decompositions over an orthonormal basis
of an inner product space
.
Here we consider that of square-integrable functions defined on an interval
of the real line
,
which is important, among others, for interpolation
theory.
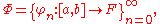
which are pairwise orthogonal for the inner product
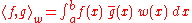
where w(x) is a weight function
, and
represents complex conjugation, i.e. 
for F=R.
The generalized Fourier series of a square-integrable function f: [a, b] → F,
with respect to Φ, is then
where the coefficients are given by
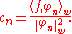
If Φ is a complete set, i.e., an orthonormal basis
of the space of all square-integrable functions on [a, b], as opposed to a smaller orthonormal set,
the relation
becomes equality in the L² sense, more precisely modulo |·|w (not necessarily pointwise, nor almost everywhere
).
and because of the theory, these polynomials are eigenfunctions of the problem and are solutions orthogonal with respect to the inner product above with unit weight. So we can form a generalized Fourier series (known as a Fourier–Legendre series) involving the Legendre polynomials, and
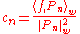
As an example, let us calculate the Fourier–Legendre series for ƒ(x) = cos x over [−1, 1]. Now,
and a series involving these terms
which differs from cos x by approximately 0.003, about 0. It may be advantageous to use such Fourier–Legendre series since the eigenfunctions are all polynomials and hence the integrals and thus the coefficients are easier to calculate.
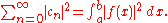
Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
, many generalizations of Fourier series
Fourier series
In mathematics, a Fourier series decomposes periodic functions or periodic signals into the sum of a set of simple oscillating functions, namely sines and cosines...
have proved to be useful.
They are all special cases of decompositions over an orthonormal basis
Orthonormal basis
In mathematics, particularly linear algebra, an orthonormal basis for inner product space V with finite dimension is a basis for V whose vectors are orthonormal. For example, the standard basis for a Euclidean space Rn is an orthonormal basis, where the relevant inner product is the dot product of...
of an inner product space
Inner product space
In mathematics, an inner product space is a vector space with an additional structure called an inner product. This additional structure associates each pair of vectors in the space with a scalar quantity known as the inner product of the vectors...
.
Here we consider that of square-integrable functions defined on an interval
Interval
Interval may refer to:* Interval , a range of numbers * Interval measurements or interval variables in statistics is a level of measurement...
of the real line
Real line
In mathematics, the real line, or real number line is the line whose points are the real numbers. That is, the real line is the set of all real numbers, viewed as a geometric space, namely the Euclidean space of dimension one...
,
which is important, among others, for interpolation
Interpolation
In the mathematical field of numerical analysis, interpolation is a method of constructing new data points within the range of a discrete set of known data points....
theory.
Definition
Consider a set of square-integrable functions with values in F=C or R,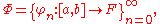which are pairwise orthogonal for the inner product
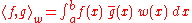
where w(x) is a weight function
Weight function
A weight function is a mathematical device used when performing a sum, integral, or average in order to give some elements more "weight" or influence on the result than other elements in the same set. They occur frequently in statistics and analysis, and are closely related to the concept of a...
, and
represents complex conjugation, i.e. for F=R.The generalized Fourier series of a square-integrable function f: [a, b] → F,
with respect to Φ, is then
where the coefficients are given by
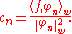
If Φ is a complete set, i.e., an orthonormal basis
Orthonormal basis
In mathematics, particularly linear algebra, an orthonormal basis for inner product space V with finite dimension is a basis for V whose vectors are orthonormal. For example, the standard basis for a Euclidean space Rn is an orthonormal basis, where the relevant inner product is the dot product of...
of the space of all square-integrable functions on [a, b], as opposed to a smaller orthonormal set,
the relation
becomes equality in the L² sense, more precisely modulo |·|w (not necessarily pointwise, nor almost everywhereAlmost everywhere
In measure theory , a property holds almost everywhere if the set of elements for which the property does not hold is a null set, that is, a set of measure zero . In cases where the measure is not complete, it is sufficient that the set is contained within a set of measure zero...
).
Example (Fourier–Legendre series)
The Legendre polynomials are solutions to the Sturm–Liouville problem
and because of the theory, these polynomials are eigenfunctions of the problem and are solutions orthogonal with respect to the inner product above with unit weight. So we can form a generalized Fourier series (known as a Fourier–Legendre series) involving the Legendre polynomials, and
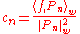
As an example, let us calculate the Fourier–Legendre series for ƒ(x) = cos x over [−1, 1]. Now,
and a series involving these terms
which differs from cos x by approximately 0.003, about 0. It may be advantageous to use such Fourier–Legendre series since the eigenfunctions are all polynomials and hence the integrals and thus the coefficients are easier to calculate.
Parseval's theorem
If Φ is a complete set,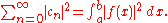See also
- OrthogonalityOrthogonalityOrthogonality occurs when two things can vary independently, they are uncorrelated, or they are perpendicular.-Mathematics:In mathematics, two vectors are orthogonal if they are perpendicular, i.e., they form a right angle...
- Orthogonal function
- Eigenfunctions
- Vector spaceVector spaceA vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
- Function spaceFunction spaceIn mathematics, a function space is a set of functions of a given kind from a set X to a set Y. It is called a space because in many applications it is a topological space, a vector space, or both.-Examples:...
- Topological vector spaceTopological vector spaceIn mathematics, a topological vector space is one of the basic structures investigated in functional analysis...
- Hilbert spaceHilbert spaceThe mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
- Banach spaceBanach spaceIn mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...