
Generalized Hebbian Algorithm
Encyclopedia
The Generalized Hebbian Algorithm (GHA), also known in the literature as Sanger's rule, is a linear feedforward neural network
model for unsupervised learning with applications primarily in principal components analysis
. First defined in 1989, it is similar to Oja's rule
in its formulation and stability, except it can be applied to networks with multiple outputs.
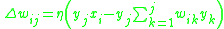 ,
,
where defines the synaptic weight
or connection strength between the th input and th output neurons, and are the input and output vectors, respectively, and is the learning rate parameter.
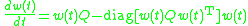 ,
,
and the Gram-Schmidt algorithm is
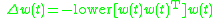 ,
,
where is any matrix, in this case representing synaptic weights, is the autocorrelation matrix, simply the outer product of inputs, is the function that diagonalizes
a matrix, and is the function that sets all matrix elements on or above the diagonal equal to 0. We can combine these equations to get our original rule in matrix form,
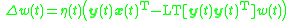 ,
,
where the function sets all matrix elements above the diagonal equal to 0, and note that our output is a linear neuron.
is necessary, or where a feature or principal components analysis can be used. Examples of such cases include artificial intelligence
and speech and image processing.
Its importance comes from the fact that learning is a single-layer process--that is, a synaptic weight changes only depending on the response of the inputs and outputs of that layer, thus avoiding the multi-layer dependence associated with the backpropagation
algorithm. It also has a simple and predictable trade-off between learning speed and accuracy of convergence as set by the learning rate parameter .
Neural network
The term neural network was traditionally used to refer to a network or circuit of biological neurons. The modern usage of the term often refers to artificial neural networks, which are composed of artificial neurons or nodes...
model for unsupervised learning with applications primarily in principal components analysis
Principal components analysis
Principal component analysis is a mathematical procedure that uses an orthogonal transformation to convert a set of observations of possibly correlated variables into a set of values of uncorrelated variables called principal components. The number of principal components is less than or equal to...
. First defined in 1989, it is similar to Oja's rule
Oja's rule
Oja's learning rule, or simply Oja's rule, named after a Finnish computer scientist Erkki Oja, is a model of how neurons in the brain or in artificial neural networks change connection strength, or learn, over time...
in its formulation and stability, except it can be applied to networks with multiple outputs.
Theory
GHA combines Oja's rule with the Gram-Schmidt process to produce a learning rule of the form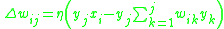 ,
,where defines the synaptic weight
Synaptic weight
In neuroscience and computer science, synaptic weight refers to the strength or amplitude of a connection between two nodes, corresponding in biology to the amount of influence the firing of one neuron has on another...
or connection strength between the th input and th output neurons, and are the input and output vectors, respectively, and is the learning rate parameter.
Derivation
In matrix form, Oja's rule can be written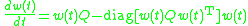 ,
,and the Gram-Schmidt algorithm is
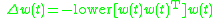 ,
,where is any matrix, in this case representing synaptic weights, is the autocorrelation matrix, simply the outer product of inputs, is the function that diagonalizes
Diagonalization
In mathematics, diagonalization may refer to:* Diagonal matrix, which is in a form with nonzero entries only on the main diagonal* Diagonalizable matrix, which can be put into a form with nonzero entries only on the main diagonal...
a matrix, and is the function that sets all matrix elements on or above the diagonal equal to 0. We can combine these equations to get our original rule in matrix form,
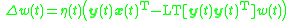 ,
,where the function sets all matrix elements above the diagonal equal to 0, and note that our output is a linear neuron.
Applications
GHA is used in applications where a self-organizing mapSelf-organizing map
A self-organizing map or self-organizing feature map is a type of artificial neural network that is trained using unsupervised learning to produce a low-dimensional , discretized representation of the input space of the training samples, called a map...
is necessary, or where a feature or principal components analysis can be used. Examples of such cases include artificial intelligence
Artificial intelligence
Artificial intelligence is the intelligence of machines and the branch of computer science that aims to create it. AI textbooks define the field as "the study and design of intelligent agents" where an intelligent agent is a system that perceives its environment and takes actions that maximize its...
and speech and image processing.
Its importance comes from the fact that learning is a single-layer process--that is, a synaptic weight changes only depending on the response of the inputs and outputs of that layer, thus avoiding the multi-layer dependence associated with the backpropagation
Backpropagation
Backpropagation is a common method of teaching artificial neural networks how to perform a given task. Arthur E. Bryson and Yu-Chi Ho described it as a multi-stage dynamic system optimization method in 1969 . It wasn't until 1974 and later, when applied in the context of neural networks and...
algorithm. It also has a simple and predictable trade-off between learning speed and accuracy of convergence as set by the learning rate parameter .

