
Generalized Helmholtz theorem
Encyclopedia
The generalized Helmholtz theorem is the multi-dimensional generalization of the Helmholtz theorem which is valid only in one dimension. The generalized Helmholtz theorem reads as follows.
Let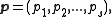
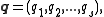
be the canonical coordinates
of a s-dimensional Hamiltonian system
, and let
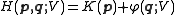
be the Hamiltonian
function, where
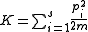 ,
,
is the kinetic energy
and
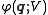
is the potential energy
which depends on a parameter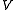 .
.
Let the hyper-surfaces of constant energy in the 2s-dimensional phase space of the system be metrically indecomposable and let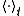 denote time average. Define the quantities
denote time average. Define the quantities 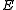 ,
, 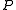 ,
, 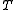 ,
, 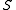 , as follows:
, as follows:
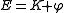 ,
,
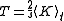 ,
,
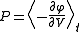 ,
,
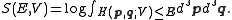
Then:
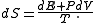
reads exactly as the heat theorem of thermodynamics
. This fact shows that thermodynamic-like relations exist between certain mechanical quantities in multidimensional ergodic systems. This in turn allows to define the "thermodynamic state" of a multi-dimensional ergodic mechanical system, without the requirement that the system be composed of a large number of degrees of freedom. In particular the temperature
 is given by twice the time average of the kinetic energy per degree of freedom, and the entropy
is given by twice the time average of the kinetic energy per degree of freedom, and the entropy
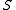 by the logarithm of the phase space volume enclosed by the constant energy surface (i.e. the so-called volume entropy
by the logarithm of the phase space volume enclosed by the constant energy surface (i.e. the so-called volume entropy
.
Let
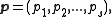
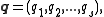
be the canonical coordinates
Canonical coordinates
In mathematics and classical mechanics, canonical coordinates are particular sets of coordinates on the phase space, or equivalently, on the cotangent manifold of a manifold. Canonical coordinates arise naturally in physics in the study of Hamiltonian mechanics...
of a s-dimensional Hamiltonian system
Hamiltonian system
In physics and classical mechanics, a Hamiltonian system is a physical system in which forces are momentum invariant. Hamiltonian systems are studied in Hamiltonian mechanics....
, and let
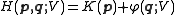
be the Hamiltonian
Hamiltonian
Hamiltonian may refer toIn mathematics :* Hamiltonian system* Hamiltonian path, in graph theory** Hamiltonian cycle, a special case of a Hamiltonian path* Hamiltonian group, in group theory* Hamiltonian...
function, where
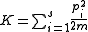 ,
,is the kinetic energy
Kinetic energy
The kinetic energy of an object is the energy which it possesses due to its motion.It is defined as the work needed to accelerate a body of a given mass from rest to its stated velocity. Having gained this energy during its acceleration, the body maintains this kinetic energy unless its speed changes...
and
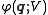
is the potential energy
Potential energy
In physics, potential energy is the energy stored in a body or in a system due to its position in a force field or due to its configuration. The SI unit of measure for energy and work is the Joule...
which depends on a parameter
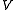 .
.Let the hyper-surfaces of constant energy in the 2s-dimensional phase space of the system be metrically indecomposable and let
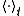 denote time average. Define the quantities
denote time average. Define the quantities 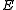 ,
, 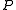 ,
, 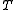 ,
, 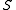 , as follows:
, as follows: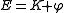 ,
,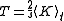 ,
,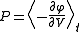 ,
,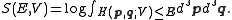
Then:
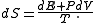
Remarks
The thesis of this theorem of classical mechanicsClassical mechanics
In physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...
reads exactly as the heat theorem of thermodynamics
Thermodynamics
Thermodynamics is a physical science that studies the effects on material bodies, and on radiation in regions of space, of transfer of heat and of work done on or by the bodies or radiation...
. This fact shows that thermodynamic-like relations exist between certain mechanical quantities in multidimensional ergodic systems. This in turn allows to define the "thermodynamic state" of a multi-dimensional ergodic mechanical system, without the requirement that the system be composed of a large number of degrees of freedom. In particular the temperature
Temperature
Temperature is a physical property of matter that quantitatively expresses the common notions of hot and cold. Objects of low temperature are cold, while various degrees of higher temperatures are referred to as warm or hot...
 is given by twice the time average of the kinetic energy per degree of freedom, and the entropy
is given by twice the time average of the kinetic energy per degree of freedom, and the entropyEntropy
Entropy is a thermodynamic property that can be used to determine the energy available for useful work in a thermodynamic process, such as in energy conversion devices, engines, or machines. Such devices can only be driven by convertible energy, and have a theoretical maximum efficiency when...
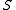 by the logarithm of the phase space volume enclosed by the constant energy surface (i.e. the so-called volume entropy
by the logarithm of the phase space volume enclosed by the constant energy surface (i.e. the so-called volume entropyVolume entropy
The volume entropy is an asymptotic invariant of a compact Riemannian manifold that measures the exponential growth rate of the volume of metric balls in its universal cover. This concept is closely related with other notions of entropy found in dynamical systems and plays an important role in...
.
Further reading
- Helmholtz, H., von (1884a). Principien der Statik monocyklischer Systeme. Borchardt-Crelle’s Journal für die reine und angewandte Mathematik, 97, 111–140 (also in Wiedemann G. (Ed.) (1895) Wissenschafltliche Abhandlungen. Vol. 3 (pp. 142–162, 179–202). Leipzig: Johann Ambrosious Barth).
- Helmholtz, H., von (1884b). Studien zur Statik monocyklischer Systeme. Sitzungsberichte der Kö niglich Preussischen Akademie der Wissenschaften zu Berlin, I, 159–177 (also in Wiedemann G. (Ed.) (1895) Wissenschafltliche Abhandlungen. Vol. 3 (pp. 163–178). Leipzig: Johann Ambrosious Barth).
- Boltzmann, L. (1884). Über die Eigenschaften monocyklischer und anderer damit verwandter Systeme.Crelles Journal, 98: 68–94 (also in Boltzmann, L. (1909). Wissenschaftliche Abhandlungen (Vol. 3,pp. 122–152), F. Hasenöhrl (Ed.). Leipzig. Reissued New York: Chelsea, 1969).
- Khinchin, A. I. (1949). Mathematical foundations of statistical mechanics. New York: Dover.
- Gallavotti, G. (1999). Statistical mechanics: A short treatise. Berlin: Springer.
- Campisi, M. (2005) On the mechanical foundations of thermodynamics: The generalized Helmholtz theorem Studies in History and Philosophy of Modern Physics 36: 275–290

