Generalized inverse Gaussian distribution
Encyclopedia
In probability theory
and statistics
, the generalized inverse Gaussian distribution (GIG) is a three-parameter family of continuous probability distribution
s with probability density function
where Kp is a modified Bessel function of the second kind, a > 0, b > 0 and p a real parameter. It is used extensively in geostatistics
, statistical linguistics, finance, etc. This distribution was first proposed by Etienne Halphen. It was rediscovered and popularised by Ole Barndorff-Nielsen, who called it the generalized inverse Gaussian distribution, and Herbert Sichel
. It is also known as the Sichel distribution. Its statistical properties are discussed in Bent Jørgensen's lecture notes.
The inverse Gaussian
and gamma distributions are special cases of the generalized inverse Gaussian distribution for p = -1/2 and b = 0, respectively.
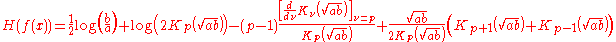
where
is a derivative of the modified Bessel function of the second kind with respect to the order 
evaluated at 
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
and statistics
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, the generalized inverse Gaussian distribution (GIG) is a three-parameter family of continuous probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
s with probability density function
Probability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
where Kp is a modified Bessel function of the second kind, a > 0, b > 0 and p a real parameter. It is used extensively in geostatistics
Geostatistics
Geostatistics is a branch of statistics focusing on spatial or spatiotemporal datasets. Developed originally to predict probability distributions of ore grades for mining operations, it is currently applied in diverse disciplines including petroleum geology, hydrogeology, hydrology, meteorology,...
, statistical linguistics, finance, etc. This distribution was first proposed by Etienne Halphen. It was rediscovered and popularised by Ole Barndorff-Nielsen, who called it the generalized inverse Gaussian distribution, and Herbert Sichel
Herbert Sichel
Dr Herbert Sichel was a statistician who made great advances in the areas of both theoretical and applied statistics.He developed the Sichel-t Estimator for the Log-normal distribution's t-statistic...
. It is also known as the Sichel distribution. Its statistical properties are discussed in Bent Jørgensen's lecture notes.
The inverse Gaussian
Inverse Gaussian distribution
| cdf = \Phi\left +\exp\left \Phi\left...
and gamma distributions are special cases of the generalized inverse Gaussian distribution for p = -1/2 and b = 0, respectively.
Entropy
The entropy of the generalized inverse Gaussian distribution is given as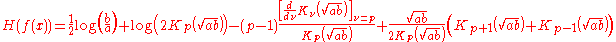where
is a derivative of the modified Bessel function of the second kind with respect to the order evaluated at See also
- Inverse Gaussian distributionInverse Gaussian distribution| cdf = \Phi\left +\exp\left \Phi\left...
- Gamma distribution